题目内容
 选修4-1:几何证明选讲
选修4-1:几何证明选讲如图,E是圆O中直径CF延长线上一点,弦AB⊥CF,AE交圆O于P,PB交CF于D,连接AO、AD.求证:
(Ⅰ)∠E=∠OAD;
(Ⅱ)OF2=OD•OE.
考点:与圆有关的比例线段
专题:直线与圆
分析:(Ⅰ)由已知条件,结合图形知∠E=∠APD-∠PDE,∠OAD=∠APD-∠ADC,再由垂径定理能证明∠E=∠OAD.
(Ⅱ)由已知条件推导出△AOD∽△EOA,由此能够证明OF2=OD•OE.
(Ⅱ)由已知条件推导出△AOD∽△EOA,由此能够证明OF2=OD•OE.
解答:
(本小题满分10分)
证明:(Ⅰ)∵E是圆O中直径CF延长线上一点,弦AB⊥CF,
∴∠CDB=∠ADC,∠AOC=∠APD,
∵∠E=∠APD-∠PDE,
∠OAD=∠AOC-∠ADC=∠APD-∠ADC,
∠PDE=∠CDB=∠ADC,
∴∠E=∠OAD.
(Ⅱ)∵∠E=∠OAD,∠AOD=∠EOA,
∴△AOD∽△EOA,
∴
=
,即OA2=OD•OE,
又∵OA=OF,∴OF2=OD•OE.
证明:(Ⅰ)∵E是圆O中直径CF延长线上一点,弦AB⊥CF,
∴∠CDB=∠ADC,∠AOC=∠APD,
∵∠E=∠APD-∠PDE,
∠OAD=∠AOC-∠ADC=∠APD-∠ADC,
∠PDE=∠CDB=∠ADC,
∴∠E=∠OAD.
(Ⅱ)∵∠E=∠OAD,∠AOD=∠EOA,
∴△AOD∽△EOA,
∴
| OA |
| OE |
| OD |
| OA |
又∵OA=OF,∴OF2=OD•OE.
点评:本题考查角相等的证明,考查等式成立的证明,解题时要注意垂径定理、相似三角形等知识点的合理运用,是中档题.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
若16-x2≥0,则( )
| A、0≤x≤4 |
| B、-4≤x≤0 |
| C、-4≤x≤4 |
| D、x≤-4或x≥4 |
从某班50名学生中抽取6名学生进行视力状况的统计分析,下列说法正确的是( )
| A、50名学生是总体 |
| B、每个被调查的学生是个体 |
| C、抽取的6名学生的视力是一个样本 |
| D、抽取的6名学生的视力是样本容量 |
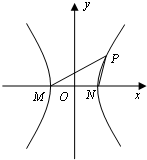 已知双曲线x2-y2=2013的左、右顶点分别为M、N,点P是双曲线上异于M、N的任意一点.
已知双曲线x2-y2=2013的左、右顶点分别为M、N,点P是双曲线上异于M、N的任意一点.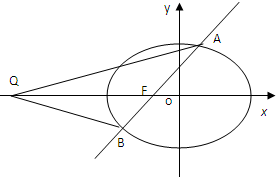 已知椭圆C:
已知椭圆C: