题目内容
已知椭圆C:
+
=1(a>b>0)的离心率e=
,短轴长为2
.
(1)求椭圆C的方程;
(2)从定点M(0,2)任作直线l与椭圆C交于两个不同的点A、B,记线段AB的中点为P,试求点P的轨迹方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
(1)求椭圆C的方程;
(2)从定点M(0,2)任作直线l与椭圆C交于两个不同的点A、B,记线段AB的中点为P,试求点P的轨迹方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
,由此能求出椭圆方程.
(2)设P(x,y),A(x1,y1),B(x2,y2),若直线l与x轴垂直,则P(0,0);若直线l与x轴不垂直,设直线l的方程为y=kx+2,k≠0.由
,得(3+4k2)x2+16kx+4=0,再由
,能求出点P的轨迹方程.
|
(2)设P(x,y),A(x1,y1),B(x2,y2),若直线l与x轴垂直,则P(0,0);若直线l与x轴不垂直,设直线l的方程为y=kx+2,k≠0.由
|
|
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)的离心率e=
,短轴长为2
,
∴
,解得a=2,b=
,
∴椭圆方程为
+
=1.
(2)设P(x,y),A(x1,y1),B(x2,y2),
若直线l与x轴垂直,则P(0,0);
若直线l与x轴不垂直,设直线l的方程为y=kx+2,k≠0.
由
,得(3+4k2)x2+16kx+4=0,…①
则
,将其消去k,得
+(y-1)2=1,
由①中△=(-16k)2-16(3+4k2)>0,解得k2>
,
则x=
=
∈[-
,0)∪(0,
],y=
+2=
∈(0,
).
综上,所求点P的轨迹方程为
+(y-1)2=1.y∈[0,
).
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
∴
|
| 3 |
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设P(x,y),A(x1,y1),B(x2,y2),
若直线l与x轴垂直,则P(0,0);
若直线l与x轴不垂直,设直线l的方程为y=kx+2,k≠0.
由
|
则
|
| 3x2 |
| 4 |
由①中△=(-16k)2-16(3+4k2)>0,解得k2>
| 1 |
| 4 |
则x=
| -8k |
| 3+4k2 |
| -8 | ||
4k+
|
2
| ||
| 3 |
2
| ||
| 3 |
| -8k2 |
| 3+4k2 |
| 6 |
| 3+4k2 |
| 3 |
| 2 |
综上,所求点P的轨迹方程为
| 3x2 |
| 4 |
| 3 |
| 2 |
点评:本题考查椭圆的方程的求法,考查点的轨迹方程的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
已知不同的直线l,m,不同的平面α,β,下命题中:
①若α∥β,l?α,则l∥β
②若α∥β,l⊥α,则l⊥β
③若l∥α,m?α,则l∥m
④若α⊥β,α∩β=l,m⊥l
则真命题的个数有( )
①若α∥β,l?α,则l∥β
②若α∥β,l⊥α,则l⊥β
③若l∥α,m?α,则l∥m
④若α⊥β,α∩β=l,m⊥l
则真命题的个数有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
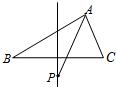 如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则
如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则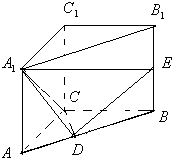 已知直三棱柱ABC-A1B1C1中,∠ACB=
已知直三棱柱ABC-A1B1C1中,∠ACB=