题目内容
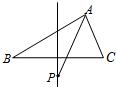如图，△ABC中，|AB|=4，|AC|=3，若P为线段BC的垂直平分线上的动点，则| AP |
| AB |
| AC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：解：设BC的中点为D，则由题意可得
=
(
+
)，
=
+
，
•(
-
)=
•
=0．
化简
•(
-
)=(
+
)•(
-
)为
(|AB|2-|AC|2)，从而求得结果．
| AD |
| 1 |
| 2 |
| AB |
| AC |
| AP |
| AD |
| DP |
| DP |
| AB |
| AC |
| DP |
| CB |
化简
| AP |
| AB |
| AC |
| AD |
| DP |
| AB |
| AC |
| 1 |
| 2 |
解答：
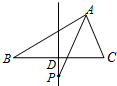解：设BC的中点为D，则
=
(
+
)，
=
+
，
可得
•(
-
)=
•
=0．
∴
•(
-
)=(
+
)•(
-
)=
•(
-
)+
(
+
)•(
-
)=
(|AB|2-|AC|2)=
，
故答案为：
．
解：设BC的中点为D，则| AD |
| 1 |
| 2 |
| AB |
| AC |
| AP |
| AD |
| DP |
可得
| DP |
| AB |
| AC |
| DP |
| CB |
∴
| AP |
| AB |
| AC |
| AD |
| DP |
| AB |
| AC |
| DP |
| AB |
| AC |
| 1 |
| 2 |
| AB |
| AC |
| AB |
| AC |
| 1 |
| 2 |
| 7 |
| 2 |
故答案为：
| 7 |
| 2 |
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
已知三个正数a，b，c，满足b＜a+c≤2b，a＜b+c≤2a，则
的取值范围是（ ）
| a |
| b |
A、（
| ||||
B、（
| ||||
C、（0，
| ||||
D、（
|
设全集U是实数集R，集合M={x|x2＞2x}，N={x|log2（x-1）≤0}，则（∁UM）∩N为（ ）
| A、{x|1＜x＜2} |
| B、{x|1≤x≤2} |
| C、{x|1＜x≤2} |
| D、{x|1≤x＜2} |
已知集合A={x∈N|0＜x＜3}，B={x|2x-1＞1}，则A∩B=（ ）
| A、∅ | B、{1} |
| C、{2} | D、{1，2} |