题目内容
已知椭圆
+
=1(a>b>0)的左右焦点为F1、F2,点P为椭圆上动点,弦PA、PB分别过点F1、F2,设向量
=λ1
,
=λ2
,求证:λ1+λ2为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| F1A |
| PF2 |
| F2B |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:由已知条件推导出|F1A|=
,|F2B|=
,对于椭圆,设CG为左准线,PC、F1E、AG分别于CG垂直,由此推导出λ1=
-1,λ2=
-1,由此能够证明λ1+λ2为定值.
| |PF1| |
| λ1 |
| |PF2| |
| λ2 |
| 2|PF1| |
| a-ec |
| 2|PF2| |
| a-ec |
解答:
证明:∵
与
同向,
与
同向,
=λ1
,
=λ2
,
∴λ1=
>0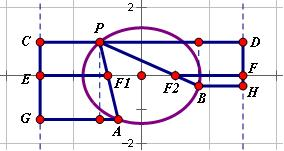 ,λ2 =
,λ2 =
>0,
∴|F1A|=
,|F2B|=
,
如图,对于椭圆,设CG为左准线,PC、F1E、AG分别于CG垂直,
e=
=
=
,
∴|PC|=
,|AG|=
,
又|EF1|=
-c=
-c为定值,
对梯形PCGA用相似三角形关系,有如下关系:
λ1 =
=
=
=
,
整理得(
-c)λ1=
-(
-c),
∴λ1=
-1,①
同理,对梯形PDHB有λ2=
-1,②
①+②,得:λ1+λ2=
-2,
对于椭圆上点P,由定义有|PF1|+|PF2|=2a,
∴λ1+λ2=
-2=
=
为定值.
| PF1 |
| F1A |
| PF2 |
| F2B |
| PF1 |
| F1A |
| PF2 |
| F2B |
∴λ1=
| ||
|
 ,λ2 =
,λ2 =
| ||
|
∴|F1A|=
| |PF1| |
| λ1 |
| |PF2| |
| λ2 |
如图,对于椭圆,设CG为左准线,PC、F1E、AG分别于CG垂直,
e=
| c |
| a |
| |PF1| |
| |PC| |
| |F1A| |
| |AG| |
∴|PC|=
| |PF1| |
| e |
| |F1A| |
| e |
又|EF1|=
| a2 |
| c |
| a |
| e |
对梯形PCGA用相似三角形关系,有如下关系:
λ1 =
| |PF1 | |
| |F1A| |
| |PC|-|EF1| |
| |EF1 |-|AG| |
| ||||
(
|
| ||||
(
|
整理得(
| a |
| e |
| 2|PF1| |
| e |
| a |
| c |
∴λ1=
| 2|PF1| |
| a-ec |
同理,对梯形PDHB有λ2=
| 2|PF2| |
| a-ec |
①+②,得:λ1+λ2=
| 2(|PF1|+|PF2|) |
| a-ec |
对于椭圆上点P,由定义有|PF1|+|PF2|=2a,
∴λ1+λ2=
| 2•2a |
| a-ec |
| 2(a+ec) |
| a-ec |
| 2(1+e2) |
| 1-e2 |
点评:本题考查两数和为定值的证明,计算量大,比较繁琐,要求熟练掌握椭圆的简单性质,解题时要认真审题,细心运算,避免出现计算上的低级错误.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x∈N|0<x<3},B={x|2x-1>1},则A∩B=( )
| A、∅ | B、{1} |
| C、{2} | D、{1,2} |