题目内容
 (1)log
(1)log| 1 |
| 2 |
| 2 |
| 3 |
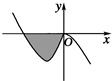
(2)已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如右图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为
| 1 |
| 12 |
考点:定积分,有理数指数幂的化简求值,指数式与对数式的互化
专题:导数的概念及应用
分析:(1)根据指数幂和对数的运算法则进行计算即可.
(2)根据函数与x轴在原点处相切,求出a,b的取值情况,然后根据积分的几何意义即可求解.
(2)根据函数与x轴在原点处相切,求出a,b的取值情况,然后根据积分的几何意义即可求解.
解答:
解:(1)log
4+(-8)
=log
(
)-2+
=-2+
=-2+4=2.
(2)∵f(x)=-x3+ax2+bx,
∴f'(x)=-3x2+2ax+b,
∵f(x)=-x3+ax2+bx(a,b∈R)的图象如右图所示,它与x轴在原点处相切,
∴f'(0)=0,即b=0,
∴f(x)=-x3+ax2,
由f(x)=-x3+ax2=0得,x=0或x=a,(a<0).
根据积分的几何意义可知阴影部分的面积S=
(0-f(x))dx=
(x3-ax2)dx=(
x4-
ax3)
=
a4-
a4=
a4=
,
解得a=-1或a=1(舍去).
故答案为:2,-1
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 | (-8)2 |
| 3 | 64 |
(2)∵f(x)=-x3+ax2+bx,
∴f'(x)=-3x2+2ax+b,
∵f(x)=-x3+ax2+bx(a,b∈R)的图象如右图所示,它与x轴在原点处相切,
∴f'(0)=0,即b=0,
∴f(x)=-x3+ax2,
由f(x)=-x3+ax2=0得,x=0或x=a,(a<0).
根据积分的几何意义可知阴影部分的面积S=
| ∫ | 0 a |
| ∫ | 0 a |
| 1 |
| 4 |
| 1 |
| 3 |
| | | 0 a |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 12 |
解得a=-1或a=1(舍去).
故答案为:2,-1
点评:本题主要考查导数的应用以及利用积分求阴影部分的面积问题,考查学生的计算能力.

练习册系列答案
相关题目
关于x的一元二次不等式ax2-5x-50>0的解集为(x1,x2),且x2-x1=15,则a=( )
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
已知恒过定点(1,1)的圆C截直线x=-1所得弦长为2,则圆心C的轨迹方程为( )
| A、x2=4x+2y |
| B、x2=4y+2x |
| C、y2=4y+2x |
| D、y2=4x+2y |
设集合A={x|x2-2x-3<0},B={x|
<2x<4},则A∩B等于( )
| 1 |
| 2 |
| A、{x|-1<x<2} |
| B、{x|-1<x<3} |
| C、{x|-3<x<2} |
| D、{x|-3<x<-1} |
 已知函数
已知函数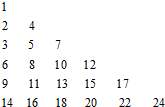 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2013,则i+j=