Question

15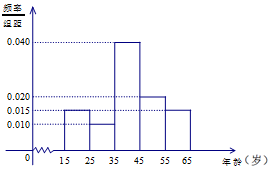．电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来，引发各方关注，收视率、点击率均占据各大排行榜首位．我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查，共调查了600人，得到结果如下：其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图；表1是不同年龄段的观众选择不同观看方式的人数． 

观看方式 年龄（岁）	电视	网络
[15，45）	150	250
[45，65]	120	80

求：（I）假设同一组中的每个数据用该组区间的中点值代替，求非常喜欢《人民的名义》这部电视剧的观众的平均年龄；
（II）根据表1，通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关？

P（K2≥k0）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k0	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

附：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

Answer 1

分析 （ I）利用频率分布直方图计算平均数即可；
（ II）根据列联表中的数据，计算K²的观测值，对照临界值即可得出结论．

解答 解：（ I）计算平均年龄为：
$\overline{x}$=20×0.15+30×0.10+40×0.40+50×0.20+60×0.15=41；  …（4分）
（ II）根据列联表中的数据，利用公式可得K²的观测值
k=$\frac{600{×（150×80-120×250）}^{2}}{270×330×400×200}$=$\frac{300}{11}$≈27.27＞6.635，…（6分）
∴有99%把握认为观看该剧的方式与年龄有关．     …（8分）

点评 本题考查了频率分布直方图与独立性检验的应用问题，是基础题．