已知函数f(x)=lnx-0.5x+1.则不等式f＜0.5的解集为( )A．{x|-1＜x＜1.5}B．{x|0.5＜x＜2}C．{x|x＜2}D．{x|1.5＜x＜2} 题目和参考答案——青夏教育精英家教网——

题目内容

4．已知函数f（x）=lnx-0.5^x+1，则不等式f（2x-3）＜0.5的解集为（　　）

A．

{x|-1＜x＜1.5}

B．

{x|0.5＜x＜2}

C．

{x|x＜2}

D．

{x|1.5＜x＜2}

分析判断f（x）的单调性，当x=1时，可得f（1）=0.5，不等式f（2x-3）＜转化为f（2x-3）＜f（1），利用单调性求解．

解答解：∵y=lnx 和y=-0.5^x在它们的定义域内都是增函数，故函数f（x）=lnx-0.5^x+1在它的定义域（0，+∞）上单调递增，
由于f（1）=0-0.5+1=0.5，故当x＞1时，f（x）＞0.5．
则不等式f（2x-3）＜0.5，即2x-3＜1 且2x-3＞0，即$\frac{3}{2}$＜x＜2，
故选：D．

点评本题考察了函数单调性的判断，“增+增等于增”和利用单调性求解不等式问题，属于中档题．

练习册系列答案

假期作业名校年度总复习暑系列答案

暑假作业暑假快乐练西安出版社系列答案

德华书业暑假训练营学年总复习安徽文艺出版社系列答案

金牌作业本南方教与学系列答案

宏翔文化暑假一本通期末加暑假加预习系列答案

乐学训练系列答案

智乐文化学业加油站暑假作业系列答案

经纶学典暑期预科班系列答案

星空小学毕业总复习系列答案

新活力总动员暑系列答案

相关题目

14．直线sinθ•x-y+1=0的倾斜角的取值范围是（　　）

$[{0，\frac{π}{4}}]∪[{\frac{3π}{4}，π}）$

$[{0，\frac{π}{4}}]$

$[{0，\frac{π}{4}}]∪（{\frac{π}{2}，π}）$

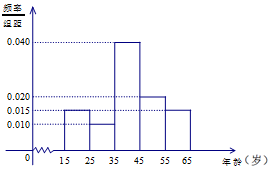电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来，引发各方关注，收视率、点击率均占据各大排行榜首位．我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查，共调查了600人，得到结果如下：其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图；表1是不同年龄段的观众选择不同观看方式的人数．

观看方式年龄（岁）	电视	网络
[15，45）	150	250
[45，65]	120	80

求：（I）假设同一组中的每个数据用该组区间的中点值代替，求非常喜欢《人民的名义》这部电视剧的观众的平均年龄；
（II）根据表1，通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关？

P（K²≥k₀）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

附：K²=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

12．函数f（x）=$\sqrt{27-{3}^{x}}$+log₂（x+2）的定义域为（　　）

19．某研究中心计划研究S市中学生的视力情况是否存在区域差异和年级差异．由数据库知S市城区和郊区的中学生人数，如表1．
表1 S市中学生人数统计

人数年级区域	7	8	9	10	11	12
城区	30000	24000	20000	16000	12500	10000
郊区	5000	4400	4000	2300	2200	1800

现用分层抽样的方法从全市中学生中抽取总量百分之一的样本，进行了调查，得到近视的学生人数如表2．
表2 S市抽样样本中近视人数统计

人数年级区域	7	8	9	10	11	12
城区	75	72	76	72	75	74
郊区	10	9	15	8	9	11

（Ⅰ）请你用独立性检验方法来研究高二（11年级）学生的视力情况是否存在城乡差异，填写2×2列联表，并判断能否在犯错误概率不超过5%的前提下认定“学生的近视情况与地区有关”．
附：

P（K²≥k₀）	0.5	0.4	0.25	0.15	0.1	0.05	0.025	0.01	0.005	0.001
k₀	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

独立性检验公式为：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
（Ⅱ）请你选择合适的角度，处理表1和表2的数据，列出所需的数据表，画出散点图，并根据散点图判断城区中学生的近视情况与年级是成正相关还是负相关．

9．在下列五个命题中：
①已知大小分别为1N与2N的两个力，要使合力大小恰为$\sqrt{6}N$，则它们的夹角为$\frac{π}{3}$；
②已知$α=\frac{2π}{5}$，$β=-\frac{π}{7}$，则sinα＜cosβ；
③若A，B，C是斜△ABC的三个内角，则恒有tanA+tanB+tanC=tanAtanBtanC成立；
④$计算式子sin{50^0}（1+\sqrt{3}tan{10^0}）的结果是\frac{1}{2}$；
⑤已知$\sqrt{3}（cosx+1）=sinx且x∈（0，\frac{3π}{2}）$，则x的大小为$\frac{2π}{3}$；
其中错误的命题有①②④⑤．（写出所有错误命题的序号）

7．（1）已知（1-x+x²）³（1-2x²）⁴=a₀+a₁x+a₂x²+…+a₁₄x¹⁴，求a₁+a₃+a₅+…+a₁₃的值．
（2）已知${（{x+1}）^2}{（{x+2}）^{2015}}={a_0}+{a_1}（{x+2}）+{a_2}{（{x+2}）^2}+…+{a_{2017}}{（{x+2}）^{2017}}$，求$\frac{a_1}{2}+\frac{a_2}{2^2}+…+\frac{{{a_{2017}}}}{{{2^{2017}}}}$的值．

4．已知函数f（x）=$\frac{{x}^{3}}{3}$+$\frac{a{x}^{2}}{2}$+2bx+c在区间（0，1）内取极大值，在区间（1，2）内取极小值，则z=（a+3）²+b²的取值范围为（$\frac{4}{5}$，9）．

5．若复数z的共轭复数$\overline z=2+i$，则复数z的模长为（　　）