题目内容
20.以平面直角坐标原点为极点,x轴正半轴为极轴,则直角坐标为(-2,2)的点的极坐标为( )| A. | (2$\sqrt{2}$,$\frac{π}{4}$) | B. | (2$\sqrt{2}$,$\frac{3π}{4}$) | C. | (2,$\frac{π}{4}$) | D. | (2,$\frac{3π}{4}$) |
分析 利用 $\left\{\begin{array}{l}{ρ=\sqrt{{x}^{2}{+y}^{2}}}\\{tanθ=\frac{y}{x}}\end{array}\right.$即可得出.
解答 解:∵ρ=$\sqrt{{(-2)}^{2}{+2}^{2}}$=2$\sqrt{2}$,tanθ=-1,
θ∈(0,π),解得θ=$\frac{3π}{4}$,
∴点M的极坐标为(2$\sqrt{2}$,$\frac{3π}{4}$).
故选:B.
点评 本题考查了直角坐标化为极坐标的方法,属于基础题.

练习册系列答案
相关题目
8.复数z=-1+2i,则z在复平面内对应的点所在象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.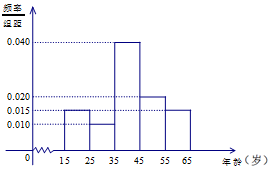 电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
 电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数. | 观看方式 年龄(岁) | 电视 | 网络 |
| [15,45) | 150 | 250 |
| [45,65] | 120 | 80 |
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
12.函数f(x)=$\sqrt{27-{3}^{x}}$+log2(x+2)的定义域为( )
| A. | (-2,3) | B. | (-2,3] | C. | (0,3) | D. | (0,3] |
 阅读程序框图,并完成下列问题:
阅读程序框图,并完成下列问题: