题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{2,x≤0}\\{\frac{4}{x},x>0}\end{array}\right.$,若函数g(x)=f(x)+x-m不存在零点,则实数m的取值范围是(2,4).分析 根据函数与方程的关系,将函数进行转化为两个函数的图象相交问题,利用数形结合进行求解即可.
解答  解:当x≤0时,g(x)=f(x)+x-m=2+x-m,
解:当x≤0时,g(x)=f(x)+x-m=2+x-m,
由g(x)=f(x)+x-m=2+x-m=0,得m=x+2,
当x>0时,(x)=f(x)+x-m=$\frac{4}{x}$+x-m,
由g(x)=f(x)+x-m=$\frac{4}{x}$+x-m=0,得m=$\frac{4}{x}$+x,
设h(x)=$\left\{\begin{array}{l}{x+2,}&{x≤0}\\{x+\frac{4}{x},}&{x>0}\end{array}\right.$,
作出函数h(x)的图象如图:
若m=h(x)没有解,
则2<m<4,
即若函数g(x)=f(x)+x-m不存在零点,则实数m的取值范围是(2,4),
故答案为:(2,4)
点评 本题主要考查函数零点的应用,根据函数与方程的关系转化为两个函数的相交问题是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列命题正确的是( )
| A. | 到x轴距离为5的点的轨迹是y=5 | |
| B. | 方程$\frac{x}{y}=1$表示的曲线是直角坐标平面上第一象限的角平分线 | |
| C. | 方程(x-y)2+(xy-1)2=0表示的曲线是一条直线和一条双曲线 | |
| D. | 2x2-3y2-2x+m=0通过原点的充要条件是m=0 |
9.函数y=$\frac{\sqrt{{x}^{2}+1}}{2x-1}$的导数是( )
| A. | $\frac{2+x}{\sqrt{{x}^{2}+1}(2x-1)^{2}}$ | B. | -$\frac{x+2}{\sqrt{{x}^{2}+1}(2x-1)^{2}}$ | ||
| C. | $\frac{4{x}^{2}-x+2}{(2x-1)^{2}}$ | D. | $\frac{4{x}^{2}-x+2}{(2x-1)^{2}\sqrt{{x}^{2}+1}}$ |
12.设全集为R,函数$f(x)=\sqrt{2-x}$的定义域为M,则∁RM为( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (-∞,2] | D. | [2,+∞) |
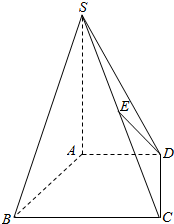 如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.
如图,在四棱锥S-ABDC中,底面ABCD是直角梯形,AB垂直于AD和BC,SA⊥底面ABCD,且SA=AB=BC=1,AD=$\frac{1}{2}$,E为SC的中点.