题目内容

13．给出下列四个命题，其中假命题的序号是（　　）
①垂直于同一条直线的两条直线互相平行
②两两相交且不过同一点的三条直线必在同一平面内
③若一个平面内有两条直线与另一个平面都平行，那么这两个平面互相平行
④与两条异面直线都相交的两条直线是异面直线．
A．①③④B．②③④C．①②③D．①②③④

分析 ①，在空间垂直于同一条直线的两条直线不一定互相平行；
②，利用直线与平面的基本性质判断A的正误；
③，若一个平面内有两条相交直线与另一个平面都平行，那么这两个平面互相平行‘’
④，根据空间两条直线的位置关系分别判断即可．

解答 解；对于①，在同一平面垂直于同一条直线的两条直线互相平行，在空间垂直于同一条直线的两条直线不一定互相平行，故①错
对于②，如图：∵a∩b=A，b∩c=B，a∩c=C，∴由两条相交直线a、b确定一个平面，不妨记为α，
∴a?α，b?α；又∵C∈a，B∈b，∴B∈α，C∈α；又∵B∈c，C∈c，
∴c?α；∴a、b、c三条直线共面．所以②正确．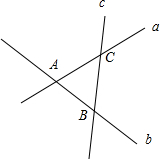
对于③，若一个平面内有两条相交直线与另一个平面都平行，
那么这两个平面互相平行，故③错
对于④：如图（1）a、b是异面直线，c、d与a、b都相交，但是cd是相交直线，所以A不正确；
如图（2）c、d是异面直线，所以C不正确；
如果c、d 平行则c、d确定唯一平面，所以a、b都在这个平面内，与a、b是异面直线矛盾，所以④不正确．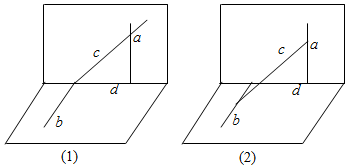

故选：A

点评 本题考查空间直线与直线的位置关系，异面直线的判断，考查空间想象能力．属于中档题．

练习册系列答案
相关题目
3．已知函数f（x）定义域为[-1，1]，若对于任意的x，y∈[-1，1]，都有f（x+y）=f（x）+f（y），且x＞0时，有f（x）＞0．
（1）证明：f（x）为奇函数；
（2）证明：f（x）在[-1，1]上单调递增；
（3）设f（1）=1，若f（x）＜m-2am+2，对所有x∈[-1，1]，a∈[-1，1]恒成立，求实数m的取值范围．
4．某产品的广告支出x（单位：万元）与销售收入y（单位：万元）之间有下表所对应的数据：
广告支出x（单位：万元）1234
销售收入y（单位：万元）12284256
（Ⅰ）求出y对x的线性回归方程；
（Ⅱ）若广告费为9万元，则销售收入约为多少万元？
（线性回归方程系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．
1．某班级要从四名男生、两名女生中选派四人参加某次社区服务，则所选的四人中至少有一名女生的选法为（　　）
A．14B．8C．6D．4
8．设f（x）为奇函数，且在（0，+∞）内是增函数，f（-2）=0，则f（x）＜0的解集为（　　）
A．（-2，0）∪（2，+∞）B．（-2，0）∪（0，2）C．（-2，0）D．（-∞，-2）∪（0，2）
18．抛物线y2=64x的准线方程为（　　）
A．x=8B．x=-8C．x=-16D．x=16
5．下列函数中，最小值为2的函数是（　　）
A．y=x+$\frac{1}{x}$B．y=sinθ+$\frac{1}{sinθ}$（0＜θ＜$\frac{π}{2}$）
C．y=sinθ+$\frac{1}{sinθ}$（0＜θ＜π）D．$\frac{1}{{\sqrt{{x^2}+2}}}+\sqrt{{x^2}+2}$
2．已知函数g（x）=lnx和函数f（x）=-x2+（a+1）x-$\frac{1}{4}$a2（其中a＜0）．
（Ⅰ）求g（log210•lg2）的值；
（Ⅱ）用max{m，n}表示m，n中的最大值，设函数h（x）=max{f（x），g（x）}（x＞0），讨论函数h（x）零点的个数．

设命题“对任意的，”，命题“存在，使”，如果命题为真，命题为假，求实数的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网