题目内容
已知a∈R,函数f(x)=a2-sinx,函数g(x)=a+1+cos2x.
(Ⅰ)若y=f(x)-g(x)在[-
,0]上的最小值是0,求a的值;
(Ⅱ)已知h(x)是定义在(-∞,+∞)上的单调减函数,若h[f(x)]<h[g(x)]对一切实数x均成立,求a的取值范围.
(Ⅰ)若y=f(x)-g(x)在[-
| π |
| 2 |
(Ⅱ)已知h(x)是定义在(-∞,+∞)上的单调减函数,若h[f(x)]<h[g(x)]对一切实数x均成立,求a的取值范围.
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:(Ⅰ)求出函数y=f(x)-g(x)的表达式,利用三角换元法求出函数在[-
,0]上的最小值建立方程关系即可求a的值;
(Ⅱ)根据函数的单调性,将不等式恒成立进行转化,求函数的最值即可.
| π |
| 2 |
(Ⅱ)根据函数的单调性,将不等式恒成立进行转化,求函数的最值即可.
解答:
解:(Ⅰ)y=f(x)-g(x)=a2-sinx-a-1-cos2x=a2-sinx-a-1-(1-sin2x)=sin2x-sinx+a2-a-2,
设t=sinx,
∵x∈[-
,0],
∴t∈[-1,0],
则函数等价为y=t2-t+a2-a-2=(t-
)2+a2-a-
则此时当t=0有最小值a2-a-2=0,
解得a=2或a=-1;
(Ⅱ)∵h(x)是定义在(-∞,+∞)上的单调减函数,
∴若h[f(x)]<h[g(x)]对一切实数x均成立,
则f(x)>g(x)对一切实数x均成立,
即f(x)-g(x)>0恒成立,
由(Ⅰ)知,即y=m(t)=t2-t+a2-a-2=(t-
)2+a2-a-
>0在t∈[-1,0]恒成立,
即函数y=m(t)=t2-t+a2-a-2=(t-
)2+a2-a-
的最小值为m(0)=a2-a-2>0恒成立,
解得a>2或a<-1.
设t=sinx,
∵x∈[-
| π |
| 2 |
∴t∈[-1,0],
则函数等价为y=t2-t+a2-a-2=(t-
| 1 |
| 2 |
| 9 |
| 4 |
则此时当t=0有最小值a2-a-2=0,
解得a=2或a=-1;
(Ⅱ)∵h(x)是定义在(-∞,+∞)上的单调减函数,
∴若h[f(x)]<h[g(x)]对一切实数x均成立,
则f(x)>g(x)对一切实数x均成立,
即f(x)-g(x)>0恒成立,
由(Ⅰ)知,即y=m(t)=t2-t+a2-a-2=(t-
| 1 |
| 2 |
| 9 |
| 4 |
即函数y=m(t)=t2-t+a2-a-2=(t-
| 1 |
| 2 |
| 9 |
| 4 |
解得a>2或a<-1.
点评:本题主要考查函数最值的应用,利用函数的单调性和最值之间的关系结合恒成立的等价转化是解决本题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
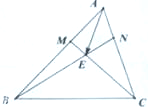 在△ABC中,已知AM:AB=1:3,AN:AC=1:4,BN与CM交于点E,
在△ABC中,已知AM:AB=1:3,AN:AC=1:4,BN与CM交于点E,