题目内容
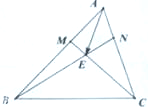在△ABC中，已知AM：AB=1：3，AN：AC=1：4，BN与CM交于点E，| AB |
| a |
| AC |
| b |
| AE |
| a |
| b |
| AE |
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：利用待定系数法设出两向量的倍数关系，选取
、
为基底，用两种不同方法表示出
，由向量相等求出点E的准确位置，即可得出答案．
| AB |
| AC |
| AE |
解答：
解：∵
=
，
=
；
设
=λ
，λ∈R，
则
=
+
=
+λ
；
而
=
-
，
∴
=
+λ（
-
）
=
+λ（
-
）；
∴
=（
-
）
+λ
；
同理，设
=t
，t∈R，
则
=
+
=
+t
=
+t（
-
）
=
+t（
-
）；
∴
=（
-
）
+t
；
∴（
-
）
+λ
=（
-
）
+t
；
由
与
是不共线向量，
∴
；
解得λ=
，t=
；
∴
=
+
．
故答案为：
+
．
| AM |
| 1 |
| 3 |
| AB |
| AN |
| 1 |
| 4 |
| AC |
设
| ME |
| MC |
则
| AE |
| AM |
| ME |
| AM |
| MC |
而
| MC |
| AC |
| AM |
∴
| AE |
| AM |
| AC |
| AM |
=
| 1 |
| 3 |
| AB |
| AC |
| 1 |
| 3 |
| AB |
∴
| AE |
| 1 |
| 3 |
| λ |
| 3 |
| AB |
| AC |
同理，设
| NE |
| NB |
则
| AE |
| AN |
| NE |
| 1 |
| 4 |
| AC |
| NB |
=
| 1 |
| 4 |
| AC |
| AB |
| AN |
=
| 1 |
| 4 |
| AC |
| AB |
| 1 |
| 4 |
| AC |
∴
| AE |
| 1 |
| 4 |
| t |
| 4 |
| AC |
| AB |
∴（
| 1 |
| 3 |
| λ |
| 3 |
| AB |
| AC |
| 1 |
| 4 |
| t |
| 4 |
| AC |
| AB |
由
| AB |
| AC |
∴
|
解得λ=
| 3 |
| 11 |
| 2 |
| 11 |
∴
| AE |
| 3 |
| 11 |
| a |
| 2 |
| 11 |
| b |
故答案为：
| 3 |
| 11 |
| a |
| 2 |
| 11 |
| b |
点评：本题考查了平面向量的线性运算与表示的问题，也考查了平面向量的基本定理的应用问题，是中档题．
练习册系列答案
导学教程高中新课标系列答案
相关题目
若函数y=sin2x与函数y=cos（x+a）在区间[
，
]上的单调性相同，则a的一个值是（ ）
| π |
| 4 |
| 3π |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
（1）已知y=|2x-2|，用“列表、描点、连线”的方式画出函数图象．设全集U=R，集合A={x|x＞-4}，B={x|x2-x-6＜0}，则A∩（∁UB）=（ ）
| A、[-2，3] |
| B、（-2，3） |
| C、（-4，-2]∪[3，+∞） |
| D、（-4，-2）∪（3，+∞） |