题目内容
函数y=lg
的定义域是 .
| x-1 |
| x+1 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由函数y的解析式,列出使函数解析式有意义的不等式组,求出解集即可.
解答:
解:∵函数y=lg
,
∴x应满足:
;
解得0<x<1,或x>1,
∴函数y的定义域是(-∞,-1)∪(1,+∞).
故答案为:(-∞,-1)∪(1,+∞).
| x-1 |
| x+1 |
∴x应满足:
|
解得0<x<1,或x>1,
∴函数y的定义域是(-∞,-1)∪(1,+∞).
故答案为:(-∞,-1)∪(1,+∞).
点评:本题考查了求函数定义域的问题,解题时应根据函数的解析式,列不等式组,求出解集,是基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
计算
dx的值是( )
| ∫ | e 1 |
| 1 |
| x |
| A、0 | B、-1 | C、2 | D、1 |
某空间几何体的三视图如图所示,则该几何体的表面积是( )
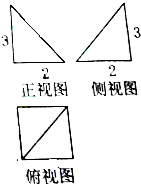

A、10+2
| ||||
B、10+2
| ||||
C、10+
| ||||
D、4+4
|
设函数f(x)=
,在区间[-
,
]上单调递增,则实数a的取值范围为( )
|
| π |
| 2 |
| π |
| 2 |
| A、1<a<2 | ||
B、
| ||
C、1<a≤
| ||
D、
|
若函数f(x)=ax4+bx2+c满足f′(1)=2,则f′(-1)=( )
| A、-1 | B、-2 | C、2 | D、0 |
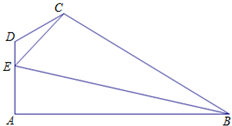 如图所示,在四边形ABCD中,AB⊥DA,CE=
如图所示,在四边形ABCD中,AB⊥DA,CE=