题目内容
某市一家庭一月份、二月份、三月份天然气用量和支付费用如下表所示:
该市的家用天然气收费方法是:天然气费=基本费+超额费+保险费.现已知,在每月用气量不超过a立方米时,只交基本费6元;用气量超过a立方米时,超过部分每立方米付b元;每户的保险费是每月c元(c≤5).设该家庭每月用气量为x立方米时,所支付的天然气费用为y元.求y关于x的函数解析式.
| 月份 | 用气量(立方米) | 支付费用(元) |
| 一 | 4 | 8 |
| 二 | 20 | 38 |
| 三 | 26 | 50 |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:根据题意,利用天然气费=基本费+超额费+保险费,把x≤a及x>a时的天然气费表示出来,再写出x的范围限制即可.
解答:
解:根据题意,y=
因为0<c≤5,所以6+c≤11.
由表格知,二、三月份的费用大于11,因此,二、三月份的用气量均超过基本量a,
于是有
解得b=2,2a=8+c.③
因为0<c≤5,所以a=
>4.
所以6+c=8,c=2.
因此,a=5,b=2,c=2.
所以,y=
.
|
因为0<c≤5,所以6+c≤11.
由表格知,二、三月份的费用大于11,因此,二、三月份的用气量均超过基本量a,
于是有
|
解得b=2,2a=8+c.③
因为0<c≤5,所以a=
| 8+c |
| 2 |
所以6+c=8,c=2.
因此,a=5,b=2,c=2.
所以,y=
|
点评:本题主要考查函数的应用,读懂题意,列出函数的表达式,注意:要根据实际意义写出自变量x的范围.

练习册系列答案
相关题目
已知数列{an}的前n项和Sn满足SnS1=Sn+1(n∈N*),且a1=2,那么a7=( )
| A、128 | B、16 | C、32 | D、64 |
如图是一个体积为4的空间几何体的三视图,则图中x的值为( )
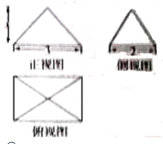

| A、2 | B、3 | C、4 | D、5 |
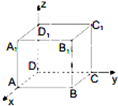 如图,把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中,使D与原点重合,点A与点C分别放在x轴和y轴的正半轴上,则B1的坐标为:( )
如图,把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中,使D与原点重合,点A与点C分别放在x轴和y轴的正半轴上,则B1的坐标为:( )| A、(2,2,2) |
| B、(2,2,0) |
| C、(2,0,2) |
| D、(0,2,2) |
复数z满足z(2+i)=2i,则在复平面内,复数z对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |