题目内容
已知向量
=(2,-1),
=(-3,4),且(m
+
)与(
-
)垂直,求实数m.
| a |
| b |
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用向量的数量积的坐标表示及向量垂直的条件:数量积为0,计算即可得到m.
解答:
解:向量
=(2,-1),
=(-3,4),
则m
+
=(2m-3,-m+4),
-
=(5,-5),
由(m
+
)与(
-
)垂直,
即有(m
+
)•(
-
)=0,
即为5(2m-3)-5(4-m)=0,
解得,m=
.
| a |
| b |
则m
| a |
| b |
| a |
| b |
由(m
| a |
| b |
| a |
| b |
即有(m
| a |
| b |
| a |
| b |
即为5(2m-3)-5(4-m)=0,
解得,m=
| 7 |
| 3 |
点评:本题考查平面向量的数量积的坐标表示,考查向量垂直的条件,考查运算能力,属于基础题.

练习册系列答案
相关题目
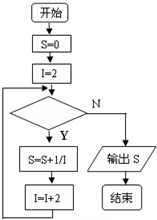
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i≤100 | B、i>100 |
| C、i>50 | D、i≤50 |
已知各项均为正数的等比数列{an}中,3a1,
a3,2a2成等差数列
=( )
| 1 |
| 2 |
| a11-a13 |
| a8-a10 |
| A、27 | B、1 |
| C、-1 | D、-1或27 |
命题“若A∩B=A,则A⊆B的逆否命题是( )
| A、若A∪B≠A,则A?B |
| B、若A∩B≠A,则A⊆B |
| C、若A⊆B,则A∩B≠A |
| D、若A?B,则A∩B≠A |