Question

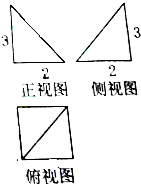
某空间几何体的三视图如图所示，则该几何体的表面积是（　　）

• A、10+2

  13

• B、10+2

  17

• C、10+

  13

  +

  17

• D、4+4

  13

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由已知的三视图可得：该几何体是一个以俯视图为底面的四棱锥，计算出各个面的面积，相加可得答案．

解答： 解：由三视图知，几何体是一个四棱锥，
四棱锥的底面是一个边长为2的正方体，
一条侧棱与底面垂直，且这条侧棱的长是3，
∴该几何体的表面积包括5部分，
S=2×2+2×

1

2

×2×3+2×

1

2

×

22+32

×2=10+2

13

，
故选：A．

点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．