题目内容
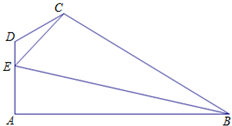 如图所示,在四边形ABCD中,AB⊥DA,CE=
如图所示,在四边形ABCD中,AB⊥DA,CE=| 7 |
| 2π |
| 3 |
| π |
| 3 |
(Ⅰ)求sin∠CED的值;
(Ⅱ)求BE的长.
考点:余弦定理,正弦定理
专题:计算题,解三角形
分析:(Ⅰ)设∠CED=α.在△CED中,由余弦定理,可解得CD=2,在△CED中,由正弦定理可解得sin∠CED的值.
(Ⅱ)由题设知α∈(0,
),先求cosα=
,而∠AEB=
-α,即可求cos∠AEB=cos(
-α)的值.
(Ⅱ)由题设知α∈(0,
| π |
| 3 |
2
| ||
| 7 |
| 2π |
| 3 |
| 2π |
| 3 |
解答:
(本小题共13分)
解:(Ⅰ)设∠CED=α.在△CED中,由余弦定理,得
CE2=CD2+DE2-2CD×DE×cos∠CDE,…(2分)
得CD2+CD-6=0,解得CD=2(CD=-3舍去).…(4分)
在△CED中,由正弦定理,得sin∠CED=
.…(6分)
(Ⅱ)由题设知α∈(0,
),所以cosα=
,…(8分)
而∠AEB=
-α,
所以cos∠AEB=cos(
-α)
=cos
cosα+sin
sinα
=-
cosα+
sinα
=-
×
+
×
=
.…(11分)
在Rt△EAB中,BE=
=4
.…(13分)
解:(Ⅰ)设∠CED=α.在△CED中,由余弦定理,得
CE2=CD2+DE2-2CD×DE×cos∠CDE,…(2分)
得CD2+CD-6=0,解得CD=2(CD=-3舍去).…(4分)
在△CED中,由正弦定理,得sin∠CED=
| ||
| 7 |
(Ⅱ)由题设知α∈(0,
| π |
| 3 |
2
| ||
| 7 |
而∠AEB=
| 2π |
| 3 |
所以cos∠AEB=cos(
| 2π |
| 3 |
=cos
| 2π |
| 3 |
| 2π |
| 3 |
=-
| 1 |
| 2 |
| ||
| 2 |
=-
| 1 |
| 2 |
2
| ||
| 7 |
| ||
| 2 |
| ||
| 7 |
=
| ||
| 14 |
在Rt△EAB中,BE=
| 2 |
| cos∠AEB |
| 7 |
点评:本题主要考查了余弦定理,正弦定理的综合应用,综合性较强,属于中档题.

练习册系列答案
相关题目
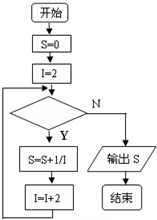
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |

| A、i≤100 | B、i>100 |
| C、i>50 | D、i≤50 |
已知直线l:y=3x-2的纵截距是( )
| A、-3 | B、-2 | C、3 | D、2 |
当a=3时,下面的程序段输出的y是( )


| A、9 | B、3 | C、10 | D、6 |
如图是一个体积为4的空间几何体的三视图,则图中x的值为( )
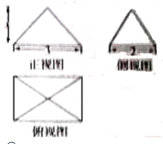

| A、2 | B、3 | C、4 | D、5 |
已知各项均为正数的等比数列{an}中,3a1,
a3,2a2成等差数列
=( )
| 1 |
| 2 |
| a11-a13 |
| a8-a10 |
| A、27 | B、1 |
| C、-1 | D、-1或27 |
命题“若A∩B=A,则A⊆B的逆否命题是( )
| A、若A∪B≠A,则A?B |
| B、若A∩B≠A,则A⊆B |
| C、若A⊆B,则A∩B≠A |
| D、若A?B,则A∩B≠A |