题目内容
设a+b=3,b>0,则当a= 时,
+
取得最小值.
| 1 |
| 3|a| |
| |a| |
| b |
考点:基本不等式
专题:不等式的解法及应用
分析:需要分类讨论,当0<a<3和当a<0,利用基本不等式即可得到结论
解答:
解:∵a+b=3,b>0,
∴b=3-a>0,即a<3,
当0<a<3时,
+
=
+
=
+
+
≥
+2
=
+
=
,当且仅当a=
取等号,
故当a=
时,
+
取得最小值;
当a<0时,
+
=-
-
=-
-
-
≥-
+2
=-
+
=
,当且仅当a=-
取等号,
故当a=-
时,
+
取得最小值;
综上所述a的值为-
时,
+
取得最小值.
故答案为:-
.
∴b=3-a>0,即a<3,
当0<a<3时,
| 1 |
| 3|a| |
| |a| |
| b |
| a+b |
| 9a |
| a |
| b |
| 1 |
| 9 |
| b |
| 9a |
| a |
| b |
| 1 |
| 9 |
|
| 1 |
| 9 |
| 2 |
| 3 |
| 7 |
| 9 |
| 3 |
| 4 |
故当a=
| 3 |
| 4 |
| 1 |
| 3|a| |
| |a| |
| b |
当a<0时,
| 1 |
| 3|a| |
| |a| |
| b |
| a+b |
| 9a |
| a |
| b |
| 1 |
| 9 |
| b |
| 9a |
| a |
| b |
| 1 |
| 9 |
|
| 1 |
| 9 |
| 2 |
| 3 |
| 5 |
| 9 |
| 3 |
| 2 |
故当a=-
| 3 |
| 2 |
| 1 |
| 3|a| |
| |a| |
| b |
综上所述a的值为-
| 3 |
| 2 |
| 1 |
| 3|a| |
| |a| |
| b |
故答案为:-
| 3 |
| 2 |
点评:本题考查了基本不等式的应用,需要分类讨论,属于中档题

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知直线l:y=3x-2的纵截距是( )
| A、-3 | B、-2 | C、3 | D、2 |
如图是一个体积为4的空间几何体的三视图,则图中x的值为( )
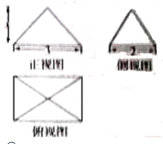

| A、2 | B、3 | C、4 | D、5 |
已知各项均为正数的等比数列{an}中,3a1,
a3,2a2成等差数列
=( )
| 1 |
| 2 |
| a11-a13 |
| a8-a10 |
| A、27 | B、1 |
| C、-1 | D、-1或27 |
设集合U={1,2,3,4},A={1,2},B={2,4},则(∁UA)∩B=( )
| A、{2} | B、{1,2,4} |
| C、{4} | D、(1,4} |