题目内容
已知函数f(x)=x3+1,关于这个函数给出以下四个命题
①函数f(x)是奇函数;
②x=0是函数f(x)的极值点;
③y=1是曲线y=f(x)的一条切线;
④存在a,b∈R,使得x∈[a,b]时,f(x)∈[a+1,b+1]
其中真命题的个数是( )
①函数f(x)是奇函数;
②x=0是函数f(x)的极值点;
③y=1是曲线y=f(x)的一条切线;
④存在a,b∈R,使得x∈[a,b]时,f(x)∈[a+1,b+1]
其中真命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,函数的性质及应用,导数的概念及应用
分析:由奇偶性的定义,即可判断①;求出导数,令它为0,检验是否极值点,即可判断②;
令f′(x)=0,得x=0,则切点为(0,1),求得切线,即可判断③;由单调性,假设存在,由f(a)=a+1,f(b)=b+1.求得a,b,即可判断④.
令f′(x)=0,得x=0,则切点为(0,1),求得切线,即可判断③;由单调性,假设存在,由f(a)=a+1,f(b)=b+1.求得a,b,即可判断④.
解答:
解:①f(-x)=-x3+1≠-f(x),故函数f(x)不是奇函数,故①错;
②f′(x)=3x2,在x=0处附近导数均大于0,故x=0不是函数f(x)的极值点,故②错;
③令f′(x)=0,得x=0,则切点为(0,1),切线为y=1.故③正确;
④由于f′(x)≥0,则f(x)在R上递增,如果存在a,b∈R,使得x∈[a,b]时,f(x)∈[a+1,b+1],
则f(a)=a+1,f(b)=b+1.则a=0,b=1或a=-1,b=1或b=0.故④正确.
故选B.
②f′(x)=3x2,在x=0处附近导数均大于0,故x=0不是函数f(x)的极值点,故②错;
③令f′(x)=0,得x=0,则切点为(0,1),切线为y=1.故③正确;
④由于f′(x)≥0,则f(x)在R上递增,如果存在a,b∈R,使得x∈[a,b]时,f(x)∈[a+1,b+1],
则f(a)=a+1,f(b)=b+1.则a=0,b=1或a=-1,b=1或b=0.故④正确.
故选B.
点评:本题考查函数的性质和运用,考查函数的奇偶性、单调性以及极值、切线问题,属于基础题.

练习册系列答案
相关题目
已知f1(x)=sinx-cosx,fn+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,fn+1(x)=fn′(x),n∈N*,则f2013(x)=( )
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4的值时,第一步算的是( )
| A、4×4=16 |
| B、7×4=28 |
| C、4×4×4=64 |
| D、7×4+6=34 |
设A=
,B=
,则A与B的大小关系是( )
| x+1 |
| x+2 |
| x+3 |
| x+4 |
| A、A<B |
| B、A>B |
| C、仅有x>0,A<B |
| D、以上结论都不成立 |
已知在二面角α-l-β的α面上有Rt△ABC,斜边BC在l上,A在β面上的射影为D,∠ABD为θ1,∠ACD为θ2,二面角α-l-β为θ.请问以下条件哪一个成立( )
| A、sin2θ=sin2θ1+sin2θ2 |
| B、cos2θ=cos2θ1+cos2θ2 |
| C、tan2θ=tan2θ1+tan2θ2 |
已知△ABC中,AB=AC=5,BC=6,则△ABC的面积为( )
| A、12 | B、15 | C、20 | D、25 |
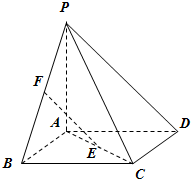 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证: