题目内容
设函数f(x)=
x3-
x2+bx+c,曲线y=f(x)在点P(0,f(0))处的切线方程为y=1
(1)确定b,c的值;
(2)若过点(0,2)可作曲线y=f(x)的三条不同切线,求a的取值范围.
| 1 |
| 3 |
| a |
| 2 |
(1)确定b,c的值;
(2)若过点(0,2)可作曲线y=f(x)的三条不同切线,求a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:(1)利用曲线f(x)在x=0处的切线方程y=1,列出方程解出b、c;
(2)构建函数,利用导数求出函数的极大值和极小值,令其极大值大于0,其极小值小于0即可解决.
(2)构建函数,利用导数求出函数的极大值和极小值,令其极大值大于0,其极小值小于0即可解决.
解答:
解:(1)求导函数可得f′(x)=x2-ax+b,
∵曲线f(x)=
x3-
x2+bx+c在x=0处的切线方程y=1,
∴f′(0)=b=0,f(0)=c=1,
∴b=0,c=1;
(2)由题意f′(x)=x2-ax.
由于点(t,f(t))处的切线方程为y-f(t)=f'(t)(x-t),
而点(0,2)在切线上,则2-f(t)=f'(t)(-t),即有
t3-
at2+1=0
设g(t)=
t3-
at2+1,g′(t)=2t2-at,则过点(0,2)可作y=f(x)的三条切线,
等价于方程2-f(t)=f'(t)(0-t)有三个相异的实根,
即等价于方程
t3-
at2+1=0有三个相异的实根①若a>0,则有

由g(t)的单调性知:要使g(t)=0有三个相异的实根,则g(0)=1>0,且g(
)=-
+1<0,
②若a<0,则g(
)>0且g(0)<0,无解.
∴a>2
.
∵曲线f(x)=
| 1 |
| 3 |
| a |
| 2 |
∴f′(0)=b=0,f(0)=c=1,
∴b=0,c=1;
(2)由题意f′(x)=x2-ax.
由于点(t,f(t))处的切线方程为y-f(t)=f'(t)(x-t),
而点(0,2)在切线上,则2-f(t)=f'(t)(-t),即有
| 2 |
| 3 |
| 1 |
| 2 |
设g(t)=
| 2 |
| 3 |
| 1 |
| 2 |
等价于方程2-f(t)=f'(t)(0-t)有三个相异的实根,
即等价于方程
| 2 |
| 3 |
| 1 |
| 2 |

由g(t)的单调性知:要使g(t)=0有三个相异的实根,则g(0)=1>0,且g(
| a |
| 2 |
| a3 |
| 24 |
②若a<0,则g(
| a |
| 2 |
∴a>2
| 3 | 3 |
点评:本题考查导数的综合运用以及数形结合的运用能力,对学生有一定的能力要求,有一定的难度

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知抛物线y2=2px,过其焦点F的直线交抛物线于A.B两点,设A.B在抛物线的准线上的射影分别是A1.B1,则∠A1FB1=( )
| A、45° | B、60° |
| C、90° | D、120° |
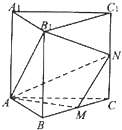 直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=
直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=