题目内容
用秦九韶算法求多项式f（x）=7x6+6x5+3x2+2当x=4的值时，第一步算的是（ ）
| A、4×4=16 |
| B、7×4=28 |
| C、4×4×4=64 |
| D、7×4+6=34 |
考点：秦九韶算法
专题：算法和程序框图
分析：根据秦九韶算法求多项式的规则变化其形式，把7x6+6x5+3x2+2等到价转化为（（（（（7x+6）x+0）x+0）x+3）x+0）x+2，就能求出结果．
解答：
解：∵f（x）=7x6+6x5+3x2+2=（（（（（7x+6）x+0）x+0）x+3）x+0）x+2，
∴在x=4时的值时，V1的值为7x+6=7×4+6=34
故选：D．
∴在x=4时的值时，V1的值为7x+6=7×4+6=34
故选：D．
点评：本题考查算法的多样性，正确理解秦九韶算法求多项式的原理是解题的关键，本题是一个比较简单的题目，运算量也不大，只要细心就能够做对．
练习册系列答案
53随堂测系列答案
相关题目
已知
和
是两个单位向量，夹角是60°，则向量2
+
和-3
+2
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、90° | B、60° |
| C、120° | D、45° |
平面向量的集合A到A的映射f(
)=
-(
•
)
，其中
为常向量．若映射f满足f(
)•f(
)=
•
对任意的
，
∈A恒成立，则
的坐标可能是（ ）
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
A、（
| ||||||||
B、（
| ||||||||
C、（
| ||||||||
D、（
|
已知抛物线y2=2px，过其焦点F的直线交抛物线于A．B两点，设A．B在抛物线的准线上的射影分别是A1．B1，则∠A1FB1=（ ）
| A、45° | B、60° |
| C、90° | D、120° |
已知θ是三角形中的最小角，则sin（θ+
）的取值范围是（ ）
| π |
| 3 |
A、（
| ||||
B、[
| ||||
C、（
| ||||
D、[
|
点P是双曲线
-
=1上的一点，F1和F2分别是双曲线的左、右焦点，
•
=0，则△F1PF2的面积是（ ）
| x2 |
| 4 |
| y2 |
| 12 |
| PF1 |
| PF2 |
| A、24 | B、16 | C、8 | D、12 |
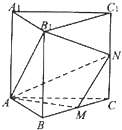直三棱柱ABC-A1B1C1中，侧棱CC1=2，∠BAC=90°，AB=AC=