题目内容
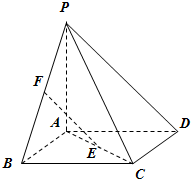 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:(Ⅰ)EF∥平面PCD;
(Ⅱ)BD⊥平面PAC.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)首先通过作辅助线利用中位线找到平行线,进一步利用线线平行转化成面面平行
(Ⅱ)通过线面垂直的性质定理转化成线线垂直,再利用线线垂直转化成线面垂直.
(Ⅱ)通过线面垂直的性质定理转化成线线垂直,再利用线线垂直转化成线面垂直.
解答:
证明:(Ⅰ)连结BD,则E是BD的中点.
又F是PB的中点,
所以EF∥PD.
因为EF?平面PCD,PD?平面PCD
所以EF∥平面PCD
(Ⅱ)∵ABCD是正方形,
∴BD⊥AC.
又PA⊥平面ABC,BD?面ABC
∴PA⊥BD.又PA∩AC=A
∴BD⊥平面PAC.

又F是PB的中点,
所以EF∥PD.
因为EF?平面PCD,PD?平面PCD
所以EF∥平面PCD
(Ⅱ)∵ABCD是正方形,
∴BD⊥AC.
又PA⊥平面ABC,BD?面ABC
∴PA⊥BD.又PA∩AC=A
∴BD⊥平面PAC.

点评:本题考查的知识点:线面平行的判定定理,线面垂直的判定和性质,属于基础题.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
平面向量的集合A到A的映射f(
)=
-(
•
)
,其中
为常向量.若映射f满足f(
)•f(
)=
•
对任意的
,
∈A恒成立,则
的坐标可能是( )
| x |
| x |
| x |
| a |
| a |
| a |
| x |
| y |
| x |
| y |
| x |
| y |
| a |
A、(
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
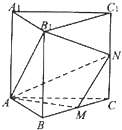 直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=
直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=