题目内容

若函数f（x）=
1
2
（ax2-ax+
1
a
）的定义域为R，求实数a的取值范围．
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：利用函数的性质求解．
解答： 解：∵函数f（x）=
1
2
（ax2-ax+
1
a
）的定义域为R，
∴a≠0，
∴实数a的取值范围是（-∞，0）∪（0，+∞）．
点评：本题考查函数的定义域的求法，是基础题，解题时要认真审题，注意函数性质的合理动作．
练习册系列答案
相关题目
已知点M（1，1）过点M作两条相互垂直的直线与圆x2+y2=4分别交于A、B、C、D，求四边形ABCD面积的最大值．
已知f（x）=
x
x2+1
在[-3，3]，判断并证明奇偶性，单调性和最值．
计算：
2lg6-lg3
1+
1
2
lg0.36+
1
3
lg8
=
 
．
解不等式：x2+（a-3）x-3a＞0．
已知函数f（x）=|x+
1
x
|，定义在R上的函数g（x）=log2（x2-4x+m），若?x1∈R，?x2∈R，使得f（x1）＞g（x2），求实数m的取值范围．
已知三条直线a，b，c，两个平面α，β．则下列命题中：
①a∥c，c∥b⇒a∥b；
②若m⊥α，m∥n，n?β⇒α⊥β；
③a∥c，c∥α⇒a∥α；
④α∥β，a∥α⇒∥β；
⑤a?α，b∥a，a∥b⇒α∥a，
正确的命题是（　　）
A、②④B、①②C、①②⑤D、③⑤
给出以下四个命题：
①△ABC中，A＞B?sinA＞sinB．
②△ABC中，A为钝角?a2＞c2+b2．
③函数y=
1
2
ln
1-cosx
1+cosx
与y=lntan
x
2
是同一函数．
④将函数y=f（x）的图象上每一点的纵坐标缩为原来的
1
2
倍，再将横坐标缩为原来的
1
2
倍，再将整个图象沿x轴向左平移
π
3
，可得y=sinx，则原函数是f（x）=2sin（2x-
π
3
）．
在上述四个命题中，真命题的序号是
 
（写出所有真命题的序号）．
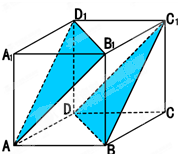已知正方体ABCD-A1B1C1D1．求证：
（1）面C1BD∥面AB1D1；
（2 ）A1C⊥平面AB1D1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网