题目内容
已知三条直线a,b,c,两个平面α,β.则下列命题中:
①a∥c,c∥b⇒a∥b;
②若m⊥α,m∥n,n?β⇒α⊥β;
③a∥c,c∥α⇒a∥α;
④α∥β,a∥α⇒∥β;
⑤a?α,b∥a,a∥b⇒α∥a,
正确的命题是( )
①a∥c,c∥b⇒a∥b;
②若m⊥α,m∥n,n?β⇒α⊥β;
③a∥c,c∥α⇒a∥α;
④α∥β,a∥α⇒∥β;
⑤a?α,b∥a,a∥b⇒α∥a,
正确的命题是( )
| A、②④ | B、①② | C、①②⑤ | D、③⑤ |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①,由公理4(平行于同一条直线的两条直线平行)可判断①正确;
②,依题意,由面面垂直的判定定理知②正确;
③,利用空间线面的位置关系可判断③错误;
④,由面面平行的性质可判断④错误;
⑤,由线面平行的判定定理,可判断⑤正确.
②,依题意,由面面垂直的判定定理知②正确;
③,利用空间线面的位置关系可判断③错误;
④,由面面平行的性质可判断④错误;
⑤,由线面平行的判定定理,可判断⑤正确.
解答:
解:对于①,a∥c,c∥b⇒a∥b,这是公理4(平行于同一条直线的两条直线平行),故①正确;
对于②,若m⊥α,m∥n,则n⊥α;
又n?β,由面面垂直的判定定理知,α⊥β,故②正确;
对于③,a∥c,c∥α⇒a∥α或a?α,故③错误;
对于④,α∥β,a∥α⇒a∥β或a?β,故④错误;
对于⑤,a?α,b∥a,b?α⇒b∥α,这是线面平行的判定定理,故⑤正确.
综上所述,正确的命题是①②⑤,
故选:C.
对于②,若m⊥α,m∥n,则n⊥α;
又n?β,由面面垂直的判定定理知,α⊥β,故②正确;
对于③,a∥c,c∥α⇒a∥α或a?α,故③错误;
对于④,α∥β,a∥α⇒a∥β或a?β,故④错误;
对于⑤,a?α,b∥a,b?α⇒b∥α,这是线面平行的判定定理,故⑤正确.
综上所述,正确的命题是①②⑤,
故选:C.
点评:本题考查命题的真假判断与应用,综合考查空间线线、线面、面面的位置关系及判定定理、性质定理的应用,考查空间想象能力与逻辑推理能力,属于中档题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知U为全集,集合M、N?U,若M∩N=N,则下列关系式中成立的是( )
| A、∁UN⊆∁UM |
| B、M⊆∁UN |
| C、∁UM⊆∁UN |
| D、∁UN⊆M |
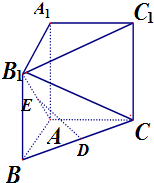 在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,∠BAC=120°,异面直线B1C与AA1成60°角,D,E分别是BC,AB1的中点.
在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,∠BAC=120°,异面直线B1C与AA1成60°角,D,E分别是BC,AB1的中点.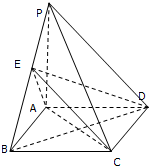 四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=
四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=