题目内容
已知数列{an}的前n项和Sn=
,n∈N*.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2 an+an,求数列{bn}的前n项和.
| n2+n |
| 2 |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2 an+an,求数列{bn}的前n项和.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)当n=1时,a1=S1=1;当n≥2时,an=Sn-Sn-1即可得出;
(2)由(1)知,bn=2n+n.利用等差数列与等比数列的前n项和公式即可得出.
(2)由(1)知,bn=2n+n.利用等差数列与等比数列的前n项和公式即可得出.
解答:
解:(1)当n=1时,a1=S1=1;
当n≥2时,an=Sn-Sn-1=
-
=n.
故数列{an}的通项公式为an=n.
(2)由(1)知,bn=2n+n.
记数列{bn}的前n项和为Tn,
则Tn=(21+22+…+2n)+(1+2+…+n)
=
+
=2n+1-2+
.
故数列{bn}的前n项和为2n+1-2+
.
当n≥2时,an=Sn-Sn-1=
| n2+n |
| 2 |
| (n-1)2+(n-1) |
| 2 |
故数列{an}的通项公式为an=n.
(2)由(1)知,bn=2n+n.
记数列{bn}的前n项和为Tn,
则Tn=(21+22+…+2n)+(1+2+…+n)
=
| 2(1-2n) |
| 1-2 |
| n(n+1) |
| 2 |
=2n+1-2+
| n(n+1) |
| 2 |
故数列{bn}的前n项和为2n+1-2+
| n(n+1) |
| 2 |
点评:本题考查了递推式的应用、等差数列与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=
的零点的个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
矩形ABCD中AB与BC长度之比为2:3,在矩形ABCD内任取一点P,则使∠APB<90°的概率为( )
A、
| ||
B、
| ||
C、1-
| ||
D、1-
|
已知点(1,1)、(0,-2)在直线x+ay+1=0的两侧,则实数a的取值范围( )
A、(-2,-
| ||
B、(-∞,-2)∪(-
| ||
C、(-2,
| ||
D、(-∞,-2)∪(
|
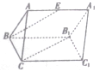 三棱柱ABC-A1B1C1的各棱相等,AA1⊥底面ABC,E是AA1的中点.
三棱柱ABC-A1B1C1的各棱相等,AA1⊥底面ABC,E是AA1的中点.