题目内容
双曲线C的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交
l1,l2于A,B两点.已知|
|=2|
|,且
与
同向.
(Ⅰ)求双曲线C的离心率;
(Ⅱ)设F(3
,0),求直线AB被双曲线C所截得的线段的长.
l1,l2于A,B两点.已知|
| OA |
| FA |
| BF |
| FA |
(Ⅰ)求双曲线C的离心率;
(Ⅱ)设F(3
| 5 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由BF⊥OB,得∠OFA=90°+α,根据正弦定理
=
,得cosα=2sinα,由此能求出双曲线的离心率.
(2)由已在得椭圆方程为
-
=1,直线AB的方程为y=-2(x-3
由此能求出AB被双曲线所截得的线段长.
|
| ||
| sin∠OFA |
|
| ||
| sin∠FOA |
(2)由已在得椭圆方程为
| x2 |
| 36 |
| y2 |
| 9 |
| 5 |
解答:
解:(1)由BF⊥OB,得∠OFA=90°+α,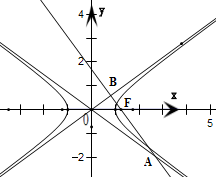
∵△OFA中,|
|=2|
|,
∴根据正弦定理
=
,
得sin∠OFA=2sin∠FOA,
即sin(90°+α)=2sinα,可得cosα=2sinα,
∴tanα=
=
,∴
=
,得a=2b,c=
=
b,
∴双曲线C的离心率e=
=
=
.
(2)∵F(3
,0),∴c=3
,
则由
=
,得a=6,b2=(3
)2-62=9,
∴椭圆方程为
-
=1,
∵l1的斜率为
=
,∴直线AB的斜率k=-2,得直线AB的方程为y=-2(x-3
),…②
将②代入①并化简,得15x2-96
x+756=0
设AB与双曲线的两交点的坐标分别为(x1,y1),(x2,y2),
则x1+x2=
,x1x2=
,…③
∴AB被双曲线所截得的线段长为:
|AB|=
•|x1-x2|=
=
=4.

∵△OFA中,|
| OA |
| FA |
∴根据正弦定理
|
| ||
| sin∠OFA |
|
| ||
| sin∠FOA |
得sin∠OFA=2sin∠FOA,
即sin(90°+α)=2sinα,可得cosα=2sinα,
∴tanα=
| sinα |
| cosα |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| a2+b2 |
| 5 |
∴双曲线C的离心率e=
| c |
| a |
| ||
| 2b |
| ||
| 2 |
(2)∵F(3
| 5 |
| 5 |
则由
| c |
| a |
| ||
| 2 |
| 5 |
∴椭圆方程为
| x2 |
| 36 |
| y2 |
| 9 |
∵l1的斜率为
| b |
| a |
| 1 |
| 2 |
| 5 |
将②代入①并化简,得15x2-96
| 5 |
设AB与双曲线的两交点的坐标分别为(x1,y1),(x2,y2),
则x1+x2=
32
| ||
| 5 |
| 252 |
| 5 |
∴AB被双曲线所截得的线段长为:
|AB|=
| 1+4 |
| 5(x1+x2)2-4x1x2 |
5×(
|
点评:本题考查双曲线的离心率的求法,考查直线被双曲线截得的线段长的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示,在河岸 ac一侧测量河的宽度,测量以下四组数据,较适宜的是( ) 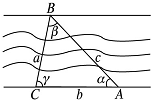

| A、c,α,γ |
| B、c,b,α |
| C、c,a,β |
| D、b,α,γ |
 某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图2所示,已知130-140分数段的人数为80,90-100分数段的人数为a,则图1所示程序框图的运算结果为( )
某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图2所示,已知130-140分数段的人数为80,90-100分数段的人数为a,则图1所示程序框图的运算结果为( )| A、700! | B、710! |
| C、720! | D、730! |
已知a>b,则下列不等式正确的是( )
| A、ac>bc | ||||
| B、a-c<b-c | ||||
| C、a3>b3 | ||||
D、
|
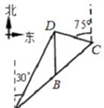 如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.
如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.