题目内容
函数f(x)=
的零点的个数为( )
|
| A、1 | B、2 | C、3 | D、4 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:求函数的导数,研究函数的极值即可判断函数零点的个数.
解答:
解:当x<0时,函数的f(x)的导数f′(x)=(x+1)ex,
则由f′(x)>0,解得-1<x<0,此时函数单调递增,
由f′(x)<0,解得x<-1,此时函数单调递减,
即当x=-1时,函数f(x)取得极小值f(-1)=-e+
<0,此时函数f(x)有2个零点,
当x≥0时,由f(x)=2x-1=0,解得x=
,
综上函数f(x)的零点个数为3个,
故选:C
则由f′(x)>0,解得-1<x<0,此时函数单调递增,
由f′(x)<0,解得x<-1,此时函数单调递减,
即当x=-1时,函数f(x)取得极小值f(-1)=-e+
| 1 |
| 3 |
当x≥0时,由f(x)=2x-1=0,解得x=
| 1 |
| 2 |
综上函数f(x)的零点个数为3个,
故选:C
点评:本题主要考查函数零点个数的判断,根据导数研究函数的极值是解决本题的关键.

练习册系列答案
相关题目
曲线C的方程为
+
=1,其中m,n是将一枚骰子先后投掷两次所得点数,事件A=“方程
+
=1表示焦点在x轴上的椭圆”,那么P(A)=( )
| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| m2 |
| y2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
空间几何体的三视图如图所示,则该几何体的表面积和体积分别为( )


A、6+2
| ||
B、8+2
| ||
C、8+2
| ||
D、6+2
|
如图所示,在河岸 ac一侧测量河的宽度,测量以下四组数据,较适宜的是( ) 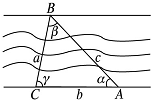

| A、c,α,γ |
| B、c,b,α |
| C、c,a,β |
| D、b,α,γ |
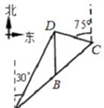 如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.
如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.