题目内容
三棱柱ABC-A1B1C1的各棱相等，AA1⊥底面ABC，E是AA1的中点．（Ⅰ）求证：BE⊥CB1；
（Ⅱ）在AB上找一点P，使P-CBE的体积等于C-ABE体积的
| 1 |
| 3 |
考点：棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题：空间位置关系与距离
分析：（Ⅰ）取AB的中点H，连结CH，HB1，由已知得CH⊥BE，BE⊥B1H，由此能证明BE⊥CB1．
（Ⅱ）
=
=
=
，根据相似三角形的关系得
=
，由此能求出点P在有向线段BA的三分之一处．
（Ⅱ）
| VP-CBE |
| VA-CBE |
| VP-CBE |
| VC-ABE |
| d1 |
| d2 |
| 1 |
| 3 |
| BP |
| BA |
| 1 |
| 3 |
解答：
（Ⅰ）证明：取AB的中点H，连结CH，HB1，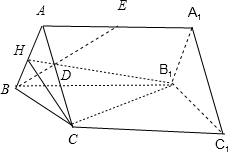
∵△ABC是等边三角形，∴CH⊥BE，
∵四边形AA1B1B是正方形，且E，H分别是AA1，AB的中点，
∴BE⊥B1H，
∵BE∩B1H=D，∴BE⊥平面CHB1，
∵CB1?平面CHB1，∴BE⊥CB1．
（Ⅱ）解：∵VC-ABE=VA-CBE，
∴
=
=
，
其中d1，d2分别是点P，A到BE的距离，
∵
=
，∴根据相似三角形的关系得
=
，
∴BP=
BA，∴点P在有向线段BA的三分之一处．
∵△ABC是等边三角形，∴CH⊥BE，
∵四边形AA1B1B是正方形，且E，H分别是AA1，AB的中点，
∴BE⊥B1H，
∵BE∩B1H=D，∴BE⊥平面CHB1，
∵CB1?平面CHB1，∴BE⊥CB1．
（Ⅱ）解：∵VC-ABE=VA-CBE，
∴
| VP-CBE |
| VA-CBE |
| VP-CBE |
| VC-ABE |
| d1 |
| d2 |
其中d1，d2分别是点P，A到BE的距离，
∵
| d1 |
| d2 |
| 1 |
| 3 |
| BP |
| BA |
| 1 |
| 3 |
∴BP=
| 1 |
| 3 |
点评：本题考查异面直线垂直的证明，考查点P的位置的确定，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
空间几何体的三视图如图所示，则该几何体的表面积和体积分别为（ ）
A、6+2
| ||
B、8+2
| ||
C、8+2
| ||
D、6+2
|
某市高三数学抽样考试中，对90分以上（含90分）的成绩进行统计，其频率分布图如图2所示，已知130-140分数段的人数为80，90-100分数段的人数为a，则图1所示程序框图的运算结果为（ ）| A、700! | B、710! |
| C、720! | D、730! |
如图，矩形长为6，宽为4，在矩形内随机地撒300颗黄豆，数得落在椭圆外的黄豆数为70颗，以此实验数据为依据，可以估计出椭圆的面积大约为（ ）