题目内容
矩形ABCD中AB与BC长度之比为2:3,在矩形ABCD内任取一点P,则使∠APB<90°的概率为( )
A、
| ||
B、
| ||
C、1-
| ||
D、1-
|
考点:几何概型
专题:概率与统计
分析:点P在矩形ABCD内,若使∠APB<90°,则P应在以AB为直径的半圆外部,所以使∠APB<90°的概率是半圆外的面积比上矩形的面积.
解答:
 解:如图,矩形ABCD中AB与BC长度之比为2:3,设AB=2,BC=3,图中白色区域是以AB为直径的半圆
解:如图,矩形ABCD中AB与BC长度之比为2:3,设AB=2,BC=3,图中白色区域是以AB为直径的半圆
当P落在半圆内时,∠APB>90°;
当P落在半圆上时,∠APB=90°;
当P落在半圆外时,∠APB<90°;
故使∠APB<90°的概率P=
=1-
=1-
;
故选:D.
 解:如图,矩形ABCD中AB与BC长度之比为2:3,设AB=2,BC=3,图中白色区域是以AB为直径的半圆
解:如图,矩形ABCD中AB与BC长度之比为2:3,设AB=2,BC=3,图中白色区域是以AB为直径的半圆当P落在半圆内时,∠APB>90°;
当P落在半圆上时,∠APB=90°;
当P落在半圆外时,∠APB<90°;
故使∠APB<90°的概率P=
| S矩形-S半圆 |
| S矩形 |
| ||
| 6 |
| π |
| 12 |
故选:D.
点评:本题考查的知识点是几何概型,关键是要画出满足条件的图形,结合图形分析,找出满足条件的点集对应的图形面积及图形的总面积.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
已知a>b,则下列不等式正确的是( )
| A、ac>bc | ||||
| B、a-c<b-c | ||||
| C、a3>b3 | ||||
D、
|
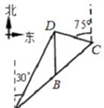 如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.
如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km. 如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为70颗,以此实验数据为依据,可以估计出椭圆的面积大约为( )
如图,矩形长为6,宽为4,在矩形内随机地撒300颗黄豆,数得落在椭圆外的黄豆数为70颗,以此实验数据为依据,可以估计出椭圆的面积大约为( )