题目内容
已知函数f(x)=
sin(x-
),x∈[0,
],那么这个函数的值域为 .
| 2 |
| 3 |
| π |
| 3 |
| π |
| 2 |
考点:三角函数的最值
专题:三角函数的求值
分析:根据x的范围求得x-
的范围,再根据正弦函数的定义域和值域求得该函数的值域.
| π |
| 3 |
解答:
解:由于x∈[0,
],∴x-
∈[-
,
],故当x-
=-
时,函数取得最小值为-
,
当x-
=
时,函数取得最大值为
,故函数的值域为[-
,
].
故答案为:[-
,
].
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| ||
| 3 |
当x-
| π |
| 3 |
| π |
| 6 |
| 1 |
| 3 |
| ||
| 3 |
| 1 |
| 3 |
故答案为:[-
| ||
| 3 |
| 1 |
| 3 |
点评:本题主要考查正弦函数的定义域和值域,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线C的方程为
+
=1,其中m,n是将一枚骰子先后投掷两次所得点数,事件A=“方程
+
=1表示焦点在x轴上的椭圆”,那么P(A)=( )
| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| m2 |
| y2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示,在河岸 ac一侧测量河的宽度,测量以下四组数据,较适宜的是( ) 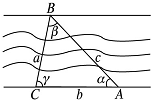

| A、c,α,γ |
| B、c,b,α |
| C、c,a,β |
| D、b,α,γ |
在0°~360°之间,与角-150°终边相同的角是( )
| A、150° | B、-30° |
| C、30° | D、210° |