题目内容
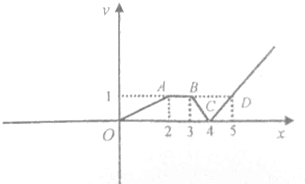
已知f(x)是定义在R上的偶函数,如图所示,线段OA,AB,BC和射线CD组成的折线是函数f(x)的部分图象,其中O为坐标原点,A(2,1)B(3,1)C(4,0)D(5,1)
(Ⅰ)求f(-1)和f(6)的值
(Ⅱ)若f(log2x-1)>f(log2x),求实数x的取值范围
(Ⅰ)求f(-1)和f(6)的值
(Ⅱ)若f(log2x-1)>f(log2x),求实数x的取值范围

考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)先求出x∈[0,1],[4,+∞)的解析式,根据偶函数的性质求解,f(-1)=f(1).
(2)因为log2x-1<log2x,再由f(log2x-1)>f(log2x),得出函数是减函数,有偶函数和图象可得.
(2)因为log2x-1<log2x,再由f(log2x-1)>f(log2x),得出函数是减函数,有偶函数和图象可得.
解答:
解:当0≤x≤2时,可求得f(x)=
x,
因为f(x)是r上的偶函数,
所以f(-1)=f(1)=
,
又C(4,0)D(5,1),结合图形可求得:
当x≥4时,f(x)=x-4,
故f(6)=6-4=2
(2)∵log2x-1<log2x,
又f(log2x-1)>f(log2x),
∴f(x)是减函数,
有图象可知:3≤log2x-1<log2x≤4,或log2x-1<log2x≤-4,-2≤log2x-1<log2x≤0,
解得:x=16,或0<x≤
,或
≤x≤1
| 1 |
| 2 |
因为f(x)是r上的偶函数,
所以f(-1)=f(1)=
| 1 |
| 2 |
又C(4,0)D(5,1),结合图形可求得:
当x≥4时,f(x)=x-4,
故f(6)=6-4=2
(2)∵log2x-1<log2x,
又f(log2x-1)>f(log2x),
∴f(x)是减函数,
有图象可知:3≤log2x-1<log2x≤4,或log2x-1<log2x≤-4,-2≤log2x-1<log2x≤0,
解得:x=16,或0<x≤
| 1 |
| 16 |
| 1 |
| 2 |
点评:本题主要考查偶函数的性质和单调性,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知a>b,则下列不等式正确的是( )
| A、ac>bc | ||||
| B、a-c<b-c | ||||
| C、a3>b3 | ||||
D、
|
在0°~360°之间,与角-150°终边相同的角是( )
| A、150° | B、-30° |
| C、30° | D、210° |
函数y=1-2x(x≤0)的值域是( )
| A、(0,1) |
| B、(-∞,1) |
| C、(0,1] |
| D、[0,1) |