题目内容
已知点(1,1)、(0,-2)在直线x+ay+1=0的两侧,则实数a的取值范围( )
A、(-2,-
| ||
B、(-∞,-2)∪(-
| ||
C、(-2,
| ||
D、(-∞,-2)∪(
|
考点:二元一次不等式(组)与平面区域
专题:不等式的解法及应用
分析:根据二元一次不等式组表示平面区域,以及A,B在直线两侧,建立不等式即可求解.
解答:
解:∵点A(1,1)与B(0,-2),在直线x+ay+1=0的两侧,
∴A,B两点对应式子x+ay+1的符号相反,
即(1+a+1)(0-2a+1)<0,
即(a+2)(1-2a)<0,
∴(a+2)(2a-1)>0,
解得a>
或a<-2,
即实数a的取值范围是(-∞,-2)∪(
,+∞),
故选:D.
∴A,B两点对应式子x+ay+1的符号相反,
即(1+a+1)(0-2a+1)<0,
即(a+2)(1-2a)<0,
∴(a+2)(2a-1)>0,
解得a>
| 1 |
| 2 |
即实数a的取值范围是(-∞,-2)∪(
| 1 |
| 2 |
故选:D.
点评:本题主要考查二元一次不等式表示平面区域,利用A,B在直线的两侧得对应式子符号相反是解决本题的关键.

练习册系列答案
相关题目
如图所示,在河岸 ac一侧测量河的宽度,测量以下四组数据,较适宜的是( ) 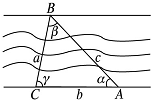

| A、c,α,γ |
| B、c,b,α |
| C、c,a,β |
| D、b,α,γ |
已知a>b,则下列不等式正确的是( )
| A、ac>bc | ||||
| B、a-c<b-c | ||||
| C、a3>b3 | ||||
D、
|
在0°~360°之间,与角-150°终边相同的角是( )
| A、150° | B、-30° |
| C、30° | D、210° |
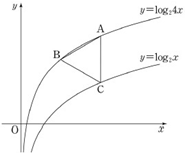 如图所示,已知函数y=log24x图象上的两点A,B和函数y=log2x上的点 C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则实数p的值为
如图所示,已知函数y=log24x图象上的两点A,B和函数y=log2x上的点 C,线段AC平行于y轴,三角形ABC为正三角形时,点B的坐标为(p,q),则实数p的值为