题目内容

某公司规定：对于小于或等于150件的订购合同，每件售价为280元，对于多于150的订购合同，每超过一件，则每件售价比原来减少1元，当公司的收益最大时订购件数为
 
．
考点：根据实际问题选择函数类型
专题：应用题,导数的综合应用
分析：设x表示销售的件数，R表示公司的收益，则R等于每件的售价x×销售件数，分类讨论，即可得出结论．
解答： 解：设x表示销售的件数，R表示公司的收益，则R等于每件的售价x×销售件数，
当x≤150时，则R≤150×280=42000
当x＞150时，则R=[280-（x-150）]x=430x-x2为公司收益，
先求R′（x）=430-2x，令R′（x）=0，得x=215时，R有最大值．
最大收益为R=430×215-（215）2=92450，
∴当公司的收益最大时订购件数为215．
故答案为：215．
点评：本题考查根据实际问题选择函数类型，考查导数知识，建立函数解析式是关键．
练习册系列答案
相关题目
y=x|x|+3的单调增区间是
 
．
已知点M（0，1），C（2，3），动点P满足|
PC
|=1，过点M且斜率为k的直线l与动点P的轨迹相交于A、B两点．
（1）求动点P的轨迹方程；
（2）求实数k的取值范围；
（3）求证：
MA
•
MB
为定值；
（4）若O为坐标原点，且
OA
•
OB
=12，求直线l的方程．
已知椭圆Г的方程为
x2
a2
+
y2
b2
=1（a＞b＞0）点A，B分别为Г上的两个动点，O为坐标原点，且OA⊥OB；其中OA，OB称为椭圆的一条半径．
（1）求证：
1
|OA|2
+
1
|OB|2
=
1
a2
+
1
b2
；|OA|2+|OB|2的最小值为
4a2b2
a2+b2
；
（2）过点O作OH⊥AB于H，求证：|OH|=
ab
a2+b2
；S△OAB的最小值是
a2b2
a2+b2
；
（3）将（1）（2）的结论推广至双曲线，结论是否依然成立，若成立，证明你的结论；若不成立，请说明理由．
已知数列{an}的前n项和Sn=
n2+n
2
，n∈N*．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=2 an+an，求数列{bn}的前n项和．
已知f（x）=logax（a＞0，a≠1）满足f[f（a2）]+f（3）=af（1）
（1）求a；
（2）计算f2（2）+f（2）f（3）+f（3）
已知函数f（x）是定义在[-3，3]上的奇函数，且f（x）在（0，1]是指数函数，在[1，3]上是二次函数，当1≤x≤3时f（x）≤f（2）=
3
2
，f（3）=
1
2
，求f（x）的解析式．
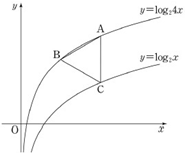如图所示，已知函数y=log24x图象上的两点A，B和函数y=log2x上的点 C，线段AC平行于y轴，三角形ABC为正三角形时，点B的坐标为（p，q），则实数p的值为
 
．
函数y=1-2x（x≤0）的值域是（　　）
A、（0，1）
B、（-∞，1）
C、（0，1]
D、[0，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网