题目内容
已知p：方程x2+mx+1=0有两个不相等的实根，q：不等式4x2+4（m-2）x+1＞0无实根．若p∨q为真命题，￢q为真命题，求实数m的取值范围．
考点：复合命题的真假
专题：简易逻辑
分析：p：方程x2+mx+1=0有两个不相等的实根，可得△=m2-4＞0，解得m．q：不等式4x2+4（m-2）x+1＞0无实根．可得△=16（m-2）2-16＜0，解得m．若p∨q为真命题，￢q为真命题，可得q为假命题，p为真命题，即可得出．
解答：
解：p：方程x2+mx+1=0有两个不相等的实根，∴△=m2-4＞0，解得m＜-2或m＞2．
q：不等式4x2+4（m-2）x+1＞0无实根．∴△=16（m-2）2-16＜0，解得1＜m＜3．
若p∨q为真命题，￢q为真命题，
∴q为假命题，p为真命题，
∴
，
解得m＜-2或m≥3．
∴实数m的取值范围是m＜-2或m≥3．
q：不等式4x2+4（m-2）x+1＞0无实根．∴△=16（m-2）2-16＜0，解得1＜m＜3．
若p∨q为真命题，￢q为真命题，
∴q为假命题，p为真命题，
∴
|
解得m＜-2或m≥3．
∴实数m的取值范围是m＜-2或m≥3．
点评：本题考查了一元二次方程的实数根与判别式的关系、复合命题真假的判定方法，考查了推理能力与计算能力，属于基础题．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
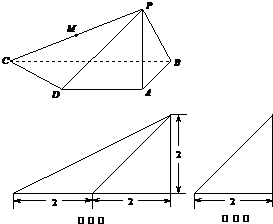四棱锥P-ABCD的直观图、主视图、侧视图如图所示，主视图是直角三角形，侧视图是等腰直角三角形，有关数据如图所示．