题目内容
方程sinx-
=0的根的个数为 .
| x |
| 2014 |
考点:根的存在性及根的个数判断,正弦函数的图象
专题:函数的性质及应用
分析:根据方程和函数之间的关系转化为函数交点个数问题即可得到结论.
解答:
解:由程sinx-
=0得程sinx=
,
设函数y=f(x)=sinx,g(x)=
,
当g(x)=1时,x=2014,
当g(x)=-1时,x=-2014,
∵320×2π≤2014<321×2π,每个周期含有2个交点,此时有321×2=642个,
∴当x<0,也有642个,
共有642×2=1284,
故答案为:1284
| x |
| 2014 |
| x |
| 2014 |
设函数y=f(x)=sinx,g(x)=
| x |
| 2014 |
当g(x)=1时,x=2014,
当g(x)=-1时,x=-2014,
∵320×2π≤2014<321×2π,每个周期含有2个交点,此时有321×2=642个,
∴当x<0,也有642个,
共有642×2=1284,
故答案为:1284
点评:本题考查方程的根与两个函数的交点的关系,体现了转化的数学思想.难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列命题中是真命题的是( )
| A、任何实数都有算术平方根 |
| B、存在三个实数,它们的和与积相等 |
| C、椭圆的离心率e越接近1时越扁,当e=1时为线段F2F2 |
| D、任意一个无理数,其平方后仍为无理数 |
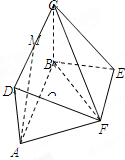 如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.
如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.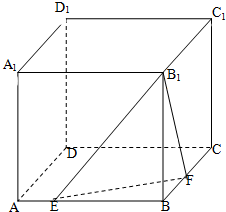 棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.
棱长为m的正方体ABCD-A1B1C1D1,E、F分别是棱AB,BC上的动点,且AE=BF.