题目内容
对于函数y=f(x)与y=g(x),在它们的公共定义域内,若f(x)-g(x)随着自变量x的增大而增大,则称函数f(x)相对于函数g(x)是“渐先函数”,下列几组函数中:
①f(x)=x与g(x)=1;
②f(x)=2x与g(x)=log2x;
③f(x)=2x与g(x)=x2;
④f(x)=ex与g(x)=log2x
函数f(x)相对于函数g(x)是“渐先函数”的有( )
①f(x)=x与g(x)=1;
②f(x)=2x与g(x)=log2x;
③f(x)=2x与g(x)=x2;
④f(x)=ex与g(x)=log2x
函数f(x)相对于函数g(x)是“渐先函数”的有( )
| A、①② | B、③④ | C、①③ | D、①④ |
考点:命题的真假判断与应用
专题:新定义,函数的性质及应用
分析:令h(x)=f(x)-g(x),根据“渐先函数”的概念对①③④四个选项逐一分析、判断即可得到答案.
解答:
解:令h(x)=f(x)-g(x),
对于①,∵h(x)=f(x)-g(x)=x-1为R上的增函数,故函数f(x)相对于函数g(x)是“渐先函数”,①正确;
对于②,∵h(x)=2x-log2x,
∴h(
)=
+1,h(1)=2-0=2,而h(
)>h(1),故函数h(x)不是增函数,即f(x)相对于函数g(x)不是“渐先函数”,②不正确;
对于③,h(x)=2x-x2;h(2)=22-22=0,h(4)=24-42=0,即h(2)=h(4),故函数h(x)不是增函数,即f(x)相对于函数g(x)不是“渐先函数”,③不正确;
对于④,f(x)=ex,g(x)=log2x,其图象如下:
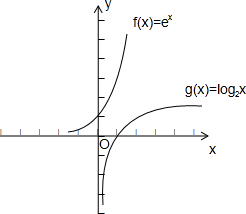
由图可知,函数f(x)相对于函数g(x)是“渐先函数”,④正确;
故选:D.
对于①,∵h(x)=f(x)-g(x)=x-1为R上的增函数,故函数f(x)相对于函数g(x)是“渐先函数”,①正确;
对于②,∵h(x)=2x-log2x,
∴h(
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
对于③,h(x)=2x-x2;h(2)=22-22=0,h(4)=24-42=0,即h(2)=h(4),故函数h(x)不是增函数,即f(x)相对于函数g(x)不是“渐先函数”,③不正确;
对于④,f(x)=ex,g(x)=log2x,其图象如下:

由图可知,函数f(x)相对于函数g(x)是“渐先函数”,④正确;
故选:D.
点评:本题考查命题的判断应用,对新定义“渐先函数”概念的理解与应用是关键,也是难点,考查分析、作图及运算求解能力,是难题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.
如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.