题目内容
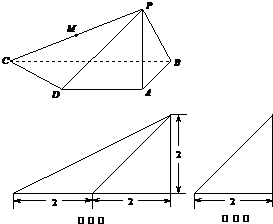 四棱锥P-ABCD的直观图、主视图、侧视图如图所示,主视图是直角三角形,侧视图是等腰直角三角形,有关数据如图所示.
四棱锥P-ABCD的直观图、主视图、侧视图如图所示,主视图是直角三角形,侧视图是等腰直角三角形,有关数据如图所示.(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)在直观图中,M是PC的中点,求证:DM∥平面PAB.
考点:直线与平面平行的判定,由三视图求面积、体积
专题:空间位置关系与距离
分析:(Ⅰ)由三视图知PA⊥AB,AD∥BC,AB=2,平面PAB⊥平面ABCD,AD⊥AB,BC=4,AD=2,得到PA⊥平面ABCD,利用四棱锥体积公式求之;
(Ⅱ)只要证明DM∥AN,利用线面平行的判定定理证明.
(Ⅱ)只要证明DM∥AN,利用线面平行的判定定理证明.
解答:
解:(Ⅰ) 由主视图和侧视图,知PA⊥AB,AD∥BC,AB=2;
平面PAB⊥平面ABCD,AD⊥AB,BC=4,AD=2.
∵PA⊥AB,平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴PA⊥平面ABCD,从而PA=2.
易知底面ABCD为直角梯形,其面积为S底面ABCD=
×(4+2)×2=6.

所以V四棱锥P-ABCD=
S底面ABCD×PA=
×6×2=4.…(4分)
(Ⅱ)如图所示,取PB中点N,
连结 DM、MN、NA.
∵M、N分别为PC、PB的中点,
∴MN∥BC,且MN=
BC,
于是MN∥AD,且MN=AD,
则四边形ADMN为平行四边形,
∴DM∥AN,
又DM?平面PAB,AN?平面PAB,所以DM∥平面PAB.…(8分)
平面PAB⊥平面ABCD,AD⊥AB,BC=4,AD=2.
∵PA⊥AB,平面PAB⊥平面ABCD,平面PAB∩平面ABCD=AB,
∴PA⊥平面ABCD,从而PA=2.
易知底面ABCD为直角梯形,其面积为S底面ABCD=
| 1 |
| 2 |

所以V四棱锥P-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅱ)如图所示,取PB中点N,
连结 DM、MN、NA.
∵M、N分别为PC、PB的中点,
∴MN∥BC,且MN=
| 1 |
| 2 |
于是MN∥AD,且MN=AD,
则四边形ADMN为平行四边形,
∴DM∥AN,
又DM?平面PAB,AN?平面PAB,所以DM∥平面PAB.…(8分)
点评:本题考查了由几何体的三视图求几何体的体积以及证明线面平行的判定定理的运用.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
下列命题中是真命题的是( )
| A、任何实数都有算术平方根 |
| B、存在三个实数,它们的和与积相等 |
| C、椭圆的离心率e越接近1时越扁,当e=1时为线段F2F2 |
| D、任意一个无理数,其平方后仍为无理数 |
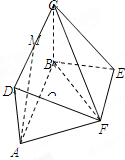 如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.
如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.