题目内容
已知三棱锥A-BCD中，AB=AC=BD=CD=2，BC=2AD=2
，则直线AD与底面BCD所成角为 ．
| 2 |
考点：直线与平面所成的角
专题：空间角
分析：根据线面角的定义，找出直线AD在底面BCD上的射影即可得到结论．
解答：
解：取BC的中点E，连结AE，DE，
∵AB=AC=BD=CD=2，
∴AE⊥BC，DE⊥BC，
则BC⊥面AED，
则AD在底面BCD的射影为DE，
则∠ADE即为直线AD与底面BCD所成的角，
∵AB=AC=BD=CD=2，BC=2AD=2
，
∴AE=
=
，DE=
，
则三角形ADE为正三角形，
则∠ADE=60°，
故答案为：60°
解：取BC的中点E，连结AE，DE，∵AB=AC=BD=CD=2，
∴AE⊥BC，DE⊥BC，
则BC⊥面AED，
则AD在底面BCD的射影为DE，
则∠ADE即为直线AD与底面BCD所成的角，
∵AB=AC=BD=CD=2，BC=2AD=2
| 2 |
∴AE=
22-(
|
| 2 |
| 2 |
则三角形ADE为正三角形，
则∠ADE=60°，
故答案为：60°
点评：本题考查异面直线所成的角，转化为平面角是解决问题关键，属中档题．
练习册系列答案
相关题目
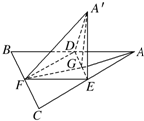如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE是△ADE绕DE旋转过程中的一个图形（点A′∉平面ABC），则下列命题中正确的是
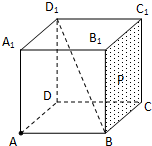如图，棱长为1的正方体ABCD-A1B1C1D1中，点P在侧面BCC1B1及其边界上运动，并且总保持向量