题目内容
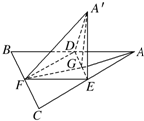 如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是
如图边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE是△ADE绕DE旋转过程中的一个图形(点A′∉平面ABC),则下列命题中正确的是①动点A′在平面ABC上的射影在线段AF上;
②BC∥平面A′DE;
③三棱锥A′-FED的体积有最大值.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离
分析:由面A′FG⊥面ABC,可知点A′在面ABC 上的射影在线段AF 上;由已知可得四边形ABCD 是菱形,从而面A′FG⊥面ABC;当面A′DE⊥面ABC 时,三棱锥A′-DEF 的体积达到最大.
解答:
解:在①中,由面A′FG⊥面ABC,
可知点A′在面ABC 上的射影在线段AF 上,∴①正确;
在②中,由已知可得四边形ABCD 是菱形,
则DE⊥GA′,DE⊥GF,
∴DE⊥平面A′FG,∴面A′FG⊥面ABC,∴②正确;
在③中,∵BC∥DE,∴BC∥平面A′DE,
当面A′DE⊥面ABC 时,三棱锥A′-DEF 的体积达到最大,
最大值为
×
×
a2×
a=
a3,∴③正确.
故答案为:①②③.
可知点A′在面ABC 上的射影在线段AF 上,∴①正确;
在②中,由已知可得四边形ABCD 是菱形,
则DE⊥GA′,DE⊥GF,
∴DE⊥平面A′FG,∴面A′FG⊥面ABC,∴②正确;
在③中,∵BC∥DE,∴BC∥平面A′DE,
当面A′DE⊥面ABC 时,三棱锥A′-DEF 的体积达到最大,
最大值为
| 1 |
| 3 |
| 1 |
| 4 |
| ||
| 4 |
| ||
| 4 |
| 1 |
| 64 |
故答案为:①②③.
点评:本题考查命题真假的判断,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
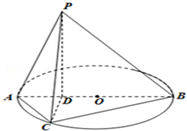 如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD=
如图所示,已知PD垂直以AB为直径的圆O所在平面,点D在线段AB上,点C为圆O上一点,且BD= 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.