Question

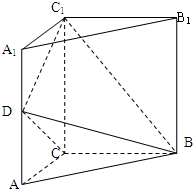如图，三棱柱ABC-A₁B₁C₁中，侧棱垂直底面，∠ACB=90°，AC=BC=

1

2

AA₁=1，D是棱AA₁的中点．
（I） 求三棱锥D-ABC的体积V_D-ABC  
（Ⅱ）证明：DC₁⊥平面BDC．

Answer 1

考点：直线与平面垂直的判定,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（I）求出棱锥的底面积和高，代入棱锥体积公式，可得V_D-ABC的体积．
（Ⅱ）在矩形ACC₁A₁中，CD=DC₁=

2

，从而C₁D⊥DC，由由题意知AB=

2

，BD=

3

，由此利用勾股定理能证明△BDC₁是直角三角形，即C₁D⊥BD，由此能证明DC₁⊥平面BDC

解答： 解：（I）∵AC=BC=

1

2

AA₁=1，D是棱AA₁的中点，
∴S_△ABC=

1

2

AC•BC=

1

2

×1×1=

1

2

，
又DA⊥平面ABC，
∴三棱锥D-ABC的体积为：V_D-ABC=

1

3

×S_△ABC×DA=

1

3

×

1

2

×1=

1

6

证明：（Ⅱ）在矩形ACC₁A₁中，CD=DC₁=

2

，
∴DC²+DC₁²=CC₁²，
△C₁DC是直角三角形，
∴C₁D⊥DC，
由题意知AB=

2

，
在Rt△ABD中，AD=1，AB=

2

，
∴BD=

3

，
在Rt△A₁DC₁中，C₁D=

A1D2+A1C12

=

2

，
在Rt△BCC₁中，BC₁=

BC2+CC12

=

5

，
∴BD²+DC₁²=BC₁²，
∴△BDC₁是直角三角形．
即C₁D⊥BD，
又∵DC∩BD=D，
∴DC₁⊥平面BDC．

点评：本题考查三角形为直角三角形和证明，考查平面和平面垂直的证明，考查三棱锥的体积的求法，解题时要认真审题，注意空间思维能力的培养．