题目内容

已知△ABC中，a=3，b=
3
，∠A=60°，则∠B等于（　　）
A、30°
B、60°
C、30°或150°
D、60°或120°
考点：正弦定理
专题：解三角形
分析：由正弦定理列出关系式，把a，b，sinA的值代入求出sinB的值，即可确定出B的度数．
解答： 解：∵△ABC中，a=3，b=
3
，∠A=60°，
∴由正弦定理
a
sinA
=
b
sinB
得：sinB=
bsinA
a
=
3
×
3
2
3
=
1
2
，
∵b＜a，∴B＜A，
则∠B=30°．
故选：A．
点评：此题考查了正弦定理，以及特殊角的三角函数值，熟练掌握正弦定理是解本题的关键．
练习册系列答案
相关题目
设△ABC的内角A，B，C所对边的长分别是a，b，c，且b=4，c=2，A=2B．
（1）求a的值；
（2）求sin(A+
π
3
)的值．
已知函数f（x）是定义在（-∞，+∞）上的奇函数．当x∈（-∞，0）时，f（x）=1-x-x4．则f（x）={
 
．
已知方程x2+2
a
•x+b=0是关于x的一元二次方程．
（Ⅰ）若a是从集合{0，1，2，3}四个数中任取的一个数，b是从集合{0，1，2}三个数中任取的一个数，求上述方程有实数根的概率；
（Ⅱ）若a∈[0，3]，b∈[0，2]，求上述方程有实数根的概率．
已知函数f（x）=lnx+x2．
（1）若函数g（x）=f（x）-ax在定义域内为增函数，求实数a的取值范围；
（2）在（1）的条件下，且a＞1，h（x）=e3x-3aex，x∈[0，ln2]，求h（x）的极小值；
（3）设F（x）=2f（x）-3x2-k（k∈R），若函数F（x）存在两个零点m，n（0＜m＜n），且满足2x0=m+n，问：函数F（x）在（x0，F（x0））处的切线能否平行于x轴？若能，求出该切线方程，若不能，请说明理由．
设a∈R，函数f（x）=cosx（asinx-cosx）+cos2（
π
2
+x）满足f(-
π
3
)=f（0）．
（1）求f（x）的单调递减区间；
（2）设锐角三角形ABC的内角A，B，C所对的边分别为a，b，c，且
a2+c2-b2
a2+b2-c2
=
c
2a-c
，求f（A）的取值范围．
已知向量
a
=（2，1），
b
=（0，-1），若（
a
-λ
b
）∥
a
，则实数λ=
 
．
一条直线的斜率范围是[-1，
3
]，则这条直线的倾斜角范围是
 
．
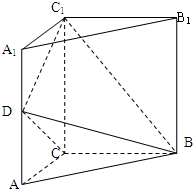如图，三棱柱ABC-A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=
1
2
AA1=1，D是棱AA1的中点．
（I） 求三棱锥D-ABC的体积VD-ABC  
（Ⅱ）证明：DC1⊥平面BDC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网