题目内容
已知圆x2+y2=1，过点P（a，0）（其中a＞1）作圆的两条切线，切点为M，N，求
•
的最小值．
| PM |
| PN |
考点：平面向量数量积的运算
专题：向量与圆锥曲线
分析：由题意画出图象，然后把
•
转化为含有a的代数式，利用基本不等式求得最小值．
| PM |
| PN |
解答：
解：如图，
•
=|
|•|
|•cos∠MPN
=(
)2•cos2∠MPO
=（a2-1）（1-2sin2∠MPO）
=(a2-1)(1-2•
)
=a2-2-1+
=a2+
-3≥2
-3=2
-3．
当且仅当a2=
，即a=
时上式取等号．
∴
•
的最小值为2
-3．
| PM |
| PN |
| PM |
| PN |
=(
| a2-1 |
=（a2-1）（1-2sin2∠MPO）
=(a2-1)(1-2•
| 1 |
| a2 |
=a2-2-1+
| 2 |
| a2 |
=a2+
| 2 |
| a2 |
a2•
|
| 2 |
当且仅当a2=
| 2 |
| a2 |
| 4 | 2 |
∴
| PM |
| PN |
| 2 |
点评：本题考查了平面向量数量积的运算，考查了数学转化思想方法，训练了利用基本不等式求最值，是中档题．
练习册系列答案
相关题目
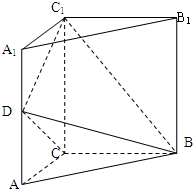如图，三棱柱ABC-A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=
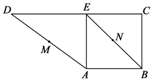如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M、N分别是AD、BE的中点，将三角形ADE沿AE折起，下列说法正确的是已知函数f（x）=|2x-1|，a＜b＜c，且f（a）＞f（c）＞f（b），则下列结论中成立的是（ ）
| A、a＜0，b＜0，c＜0 |
| B、a＜0，b≥0，c＞0 |
| C、2-a＜2c |
| D、2a+2c＜2 |