题目内容
已知曲线y=cos（ωx+
）在点（
，0）处切线斜率为k，若|k|＜1，求ω．
| π |
| 3 |
| π |
| 2 |
考点：导数的几何意义
专题：函数的性质及应用
分析：点（
，0）在曲线y=cos（ωx+
）上，求出ω的范围，在根据在点（
，0）处切线斜率为k，且|k|＜1，求出ω即可．
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答：
解：因为y=cos（ωx+
），
cos（ω
+
）=0，
ω
+
=nπ+
，
∴ω=2n+
（n∈Z），
∴y′=-ωsin（ωx+
），
∴k=y′| x=
=-（2n+
）sin[（2n+
）×
+
]═-（2n+
）sin（nπ+
）=±(2n+
)，
∵|k|＜1，
∴|2n+
|＜1，
ω=
．
| π |
| 3 |
cos（ω
| π |
| 2 |
| π |
| 3 |
ω
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴ω=2n+
| 1 |
| 3 |
∴y′=-ωsin（ωx+
| π |
| 3 |
∴k=y′| x=
| π |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| π |
| 2 |
| π |
| 3 |
| 1 |
| 3 |
| π |
| 2 |
| 1 |
| 3 |
∵|k|＜1，
∴|2n+
| 1 |
| 3 |
ω=
| 1 |
| 3 |
点评：本题考查导数的应用和三角函数的有关性质．
练习册系列答案
相关题目
已知定义在R上的函数y=f（x）满足f（-x）+f（x）=0，当x∈（-∞，0）时不等式f（x）+xf′（x）＜0总成立，若记a=20.2•f（20.2），b=（logπ3）•f（logπ3），c=（-3）•f（log3
），则a，b，c的大小关系为（ ）
| 1 |
| 27 |
| A、a＞b＞c |
| B、a＞c＞b |
| C、c＞b＞a |
| D、c＞a＞b |
设A={a}，则下列各式中正确的是（ ）
| A、0∈A | B、a∈A |
| C、a∉A | D、a=A |
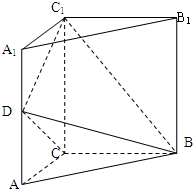如图，三棱柱ABC-A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=