题目内容
判断函数g(x)=
的奇偶性.
|
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:根据函数奇偶性的定义进行判断即可得到结论.
解答:
解:若x>0,则-x<0,
则f(-x)=-
x2-1,f(x)=
x2+1,满足f(-x)=-f(x),
若x<0,则-x>0,
则f(x)=-
x2-1,f(-x)=
x2+1,满足f(-x)=-f(x),
综上:f(-x)=-f(x),
即函数f(x)是奇函数.
则f(-x)=-
| 1 |
| 2 |
| 1 |
| 2 |
若x<0,则-x>0,
则f(x)=-
| 1 |
| 2 |
| 1 |
| 2 |
综上:f(-x)=-f(x),
即函数f(x)是奇函数.
点评:本题主要考查函数奇偶性的判断,比较基础.

练习册系列答案
相关题目
已知一个几何体的三视图如图所示,则该几何体的体积为( )


| A、2 | ||
| B、1 | ||
C、
| ||
D、
|

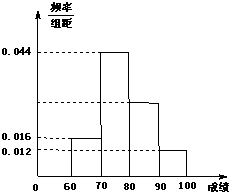 某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.
某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.