题目内容
已知椭圆C经过点(
,
),且与双曲线x2-
=1共焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于M、N两点,交y轴于P点,且记
=λ1
,
=λ2
,求证:λ1+λ2为定值.
| 2 |
| ||
| 2 |
| y2 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过椭圆C的右焦点F作直线l交椭圆C于M、N两点,交y轴于P点,且记
| PM |
| PM |
| PN |
| NF |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件设椭圆方程为
+
=1,把点(
,
)代入,能求出椭圆C的方程.
(Ⅱ)当l的斜率不为0时,设MN:x=my+
,联立
,得(m2+4)y2+2
my-1=0,设M(x1,y1),N(x2,y2),由此利用韦达定理能求出λ1+λ2=
+
=-8.当直线l的斜率为0时,λ1+λ2=-8也成立.由此能证明λ1+λ2为定值.
| x2 |
| 3+b2 |
| y2 |
| b2 |
| 2 |
| ||
| 2 |
(Ⅱ)当l的斜率不为0时,设MN:x=my+
| 3 |
|
| 3 |
y1+
| ||||
| -y1 |
y2+
| ||||
| -y2 |
解答:
(Ⅰ)解:∵双曲线x2-
=1的焦点坐标为(±
,0),
椭圆C经过点(
,
),且与双曲线x2-
=1共焦点,
∴设椭圆方程为
+
=1,
把点(
,
)代入,得
+
=1,
解得b2=1,a2=4,
∴椭圆C的方程为
+y2=1.
(Ⅱ)证明:当l的斜率不为0时,设MN:x=my+
,
联立
,得(m2+4)y2+2
my-1=0,
设M(x1,y1),N(x2,y2),则y1+y2=
,y1y2=
,
∴λ1+λ2=
+
=-2-
•(
+
)
=-2-
•
=-8.
当直线l的斜率为0时,M(2,0),N(-2,0),P(0,0),
|PM|=2,|MF|=2-
,|PN|=2,|NF|=2+
,
∴λ1+λ2=-8.
综上,λ1+λ2=-8.
∴λ1+λ2为定值-8.
| y2 |
| 2 |
| 3 |
椭圆C经过点(
| 2 |
| ||
| 2 |
| y2 |
| 2 |
∴设椭圆方程为
| x2 |
| 3+b2 |
| y2 |
| b2 |
把点(
| 2 |
| ||
| 2 |
| 2 |
| 3+b2 |
| ||
| b2 |
解得b2=1,a2=4,
∴椭圆C的方程为
| x2 |
| 4 |
(Ⅱ)证明:当l的斜率不为0时,设MN:x=my+
| 3 |
联立
|
| 3 |
设M(x1,y1),N(x2,y2),则y1+y2=
-2
| ||
| m2+4 |
| -1 |
| m2+4 |
∴λ1+λ2=
y1+
| ||||
| -y1 |
y2+
| ||||
| -y2 |
| ||
| m |
| 1 |
| y1 |
| 1 |
| y2 |
=-2-
| ||
| m |
| y1+y2 |
| y1y2 |
=-8.
当直线l的斜率为0时,M(2,0),N(-2,0),P(0,0),
|PM|=2,|MF|=2-
| 3 |
| 3 |
∴λ1+λ2=-8.
综上,λ1+λ2=-8.
∴λ1+λ2为定值-8.
点评:本题考查椭圆方程的求法,考查两数和为定值的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
 若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33+2×0=27,…,依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )
若将集合A中的数按从小到大排成数列{an},则有a1=31+2×0=3,a2=32+2×0=9,a3=32+2×1=11,a4=33+2×0=27,…,依此类推,将数列依次排成如图所示的三角形数阵,则第六行第三个数为( )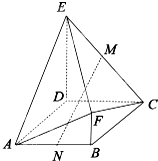 多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=
多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=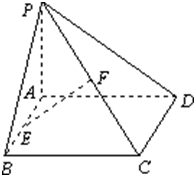 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.