题目内容
已知数列{xn},满足x1=4,xn+1=
+
,an=lg
(1)证明:数列{an}成等比数列,并求数列{xn}的通项公式;
(2)若bn=xn-2,Tn是数列{bn}的前n项和,证明:Tn<3.
| xn |
| 2 |
| 2 |
| xn |
| xn+2 |
| xn-2 |
(1)证明:数列{an}成等比数列,并求数列{xn}的通项公式;
(2)若bn=xn-2,Tn是数列{bn}的前n项和,证明:Tn<3.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)由数列递推式xn+1=
+
得到
=(
)2,借助于对数的运算性质得到数列{an}成等比数列,进一步求得数列{xn}的通项公式;
(2)把数列{xn}的通项公式代入bn=xn-2,求得bn>0,结合
<
放缩证得Tn<3.
| xn |
| 2 |
| 2 |
| xn |
| xn+1+2 |
| xn+1-2 |
| xn+2 |
| xn-2 |
(2)把数列{xn}的通项公式代入bn=xn-2,求得bn>0,结合
| bn+1 |
| bn |
| 1 |
| 3 |
解答:
证明:(1)由xn+1=
+
,知xn+1+2=
+
+2=
,
同理xn+1-2=
.
故
=(
)2,从而lg
=2lg
,
即an+1=2an.
∴数列{an}成等比数列,
故an=2n-1a1=2n-1lg
=2n-1lg3.
即lg
=2n-1lg3.
从而
=32n-1,
∴xn=
;
(2)由(1)知xn=
,
∴bn=xn-2=
>0,
∴
=
=
<
≤
=
.
当n=1时,显然T1=b1=2<3;
当n>1时,bn<
bn-1<(
)2bn-2<…<(
)n-1b1,
∴Tn=b1+b2+…+bn<b1+
b1+…+(
)n-1b1
=
=3-(
)n-1<3.
综上,Tn<3.
| xn |
| 2 |
| 2 |
| xn |
| xn |
| 2 |
| 2 |
| xn |
| (xn+2)2 |
| 2xn |
同理xn+1-2=
| (xn-2)2 |
| 2xn |
故
| xn+1+2 |
| xn+1-2 |
| xn+2 |
| xn-2 |
| xn+1+2 |
| xn+1-2 |
| xn+2 |
| xn-2 |
即an+1=2an.
∴数列{an}成等比数列,
故an=2n-1a1=2n-1lg
| x1+2 |
| x1-2 |
即lg
| xn+2 |
| xn-2 |
从而
| xn+2 |
| xn-2 |
∴xn=
| 2(32n-1+1) |
| 32n-1-1 |
(2)由(1)知xn=
| 2(32n-1+1) |
| 32n-1-1 |
∴bn=xn-2=
| 4 |
| 32n-1-1 |
∴
| bn+1 |
| bn |
| 32n-1-1 |
| 32n-1 |
| 1 |
| 32n-1+1 |
| 1 |
| 32n-1 |
| 1 |
| 321-1 |
| 1 |
| 3 |
当n=1时,显然T1=b1=2<3;
当n>1时,bn<
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴Tn=b1+b2+…+bn<b1+
| 1 |
| 3 |
| 1 |
| 3 |
=
b1[1-(
| ||
1-
|
| 1 |
| 3 |
综上,Tn<3.
点评:本题考查了数列递推式,考查了利用放缩法证明数列不等式,综合考查了学生的逻辑思维能力和灵活处理问题的能力,是中高档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
下面几种推理中是演绎推理的序号为( )
| A、半径为r圆的面积S=πr2,则单位圆的面积S=π |
| B、由金、银、铜、铁可导电,猜想:金属都可导电 |
| C、由平面三角形的性质,推测空间四面体性质 |
| D、由平面直角坐标系中圆的方程为(x-a)2+(y-b)2=r2,推测空间直角坐标系中球的方程为(x-a)2+(y-b)2+(z-c)2 |
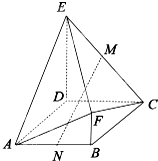 多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=
多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD= 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=