题目内容
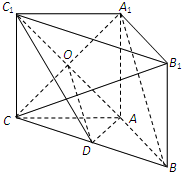
如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，D为BC中点．
（Ⅰ） 求异面直线CB1与C1A1所成的角余弦值．
（Ⅱ） 求证：A1B∥平面ADC1；
（Ⅰ） 求异面直线CB1与C1A1所成的角余弦值．
（Ⅱ） 求证：A1B∥平面ADC1；
考点：直线与平面平行的判定,异面直线及其所成的角
专题：空间位置关系与距离
分析：（Ⅰ）∠ACB1即为异面直线CB1与C1A1所成的角，解三角形可得异面直线CB1与C1A1所成的角余弦值；
（Ⅱ）利用三角形中位线的性质，证明A1B∥OD，利用线面平行的判定定理证明A1B∥平面AC1D；
（Ⅱ）利用三角形中位线的性质，证明A1B∥OD，利用线面平行的判定定理证明A1B∥平面AC1D；
解答：
解：（Ⅰ）∵三棱柱ABC-A1B1C1中，
∴C1A1∥CA，
故∠ACB1即为异面直线CB1与C1A1所成的角，
连接AB1，设AB=AC=AA1=a，
∵侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，
∴BC=AB1=
a，CB1=
a，
则△ACB1为直角三角形，
故cos∠ACB1=
=
，
证明：（Ⅱ）连结A1C，交AC1于点O，连结OD
因为ACC1A1为正方形，
所以O为AC1中点
又D为BC中点，
所以OD为△A1BC中位线
所以A1B∥OD …（6分）
因为OD?平面AC1D，AB1?平面AC1D
所以A1B∥平面AC1D…（8分）
∴C1A1∥CA，
故∠ACB1即为异面直线CB1与C1A1所成的角，
连接AB1，设AB=AC=AA1=a，
∵侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，
∴BC=AB1=
| 2 |
| 3 |
则△ACB1为直角三角形，
故cos∠ACB1=
| AC |
| CB1 |
| ||
| 3 |
证明：（Ⅱ）连结A1C，交AC1于点O，连结OD
因为ACC1A1为正方形，
所以O为AC1中点
又D为BC中点，
所以OD为△A1BC中位线
所以A1B∥OD …（6分）
因为OD?平面AC1D，AB1?平面AC1D
所以A1B∥平面AC1D…（8分）
点评：本题考查线面夹角，线面平行，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
相关题目
已知双曲线
-
=1的左右焦点分别是F1、F2，过F1的直线l与双曲线相交于A、B两点，则满足|AB|=3
的直线l有（ ）
| x2 |
| 2 |
| y2 |
| 3 |
| 2 |
| A、1条 | B、2条 | C、3条 | D、4条 |
若将集合A中的数按从小到大排成数列{an}，则有a1=31+2×0=3，a2=32+2×0=9，a3=32+2×1=11，a4=33+2×0=27，…，依此类推，将数列依次排成如图所示的三角形数阵，则第六行第三个数为（ ）
已知抛物线y2=2px（p＞0）上点M（3，m）到焦点F的距离为4．