题目内容
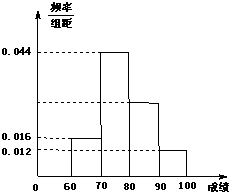 某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.
某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.(Ⅰ)求成绩在[80,90]范围内的人数;
(Ⅱ)决赛规则如下:为每位参加决赛的选手准备4道判断题,选手对其依次回答,答对两道就终止答题,并获得一等奖,若题目答完仍然只答对l道,则获得二等奖,否则获得三等奖.某同学进入决赛,每道题答对的概率p的值恰好与成绩不少于80分的频率值相同.
(i)求该同学恰好答满4道题而获得一等奖的概率;
(ii)设该同学决赛中答题个数为X,求X的分布列及X的数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由成绩在[80,90)范围内的频率是0.28,能求出成绩在[80,90)范围内的人数.
(Ⅱ)(i)由已知条件求出p=0.4.该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对1道,第4道也能够答对才获得一等奖,由此能求出结果.
(ii)由题设可知,该同学答题个数为2、3、4.即X=2、3、4,分别求出相应的概率,由此能求出X的分布列和E(X).
(Ⅱ)(i)由已知条件求出p=0.4.该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对1道,第4道也能够答对才获得一等奖,由此能求出结果.
(ii)由题设可知,该同学答题个数为2、3、4.即X=2、3、4,分别求出相应的概率,由此能求出X的分布列和E(X).
解答:
解:(Ⅰ)由已知得成绩在[80,90)范围内的频率是0.28 …(2分)
则成绩在[80,90)范围内的人数是0.28×50=14人…(3分)
(Ⅱ)∵成绩在[80,90)范围内的频率是0.28,在[90,100)范围内的频率是0.12,
∴p=0.28+0.12=0.4.…(5分)
(i)该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对1道,
第4道也能够答对才获得一等奖,
则有
×0.4×0.62×0.4=0.1728.
∴该同学恰好答满4道题而获得一等奖的概率为0.1728.…(7分)
(ii)由题设可知,该同学答题个数为2、3、4.即X=2、3、4,
P(X=2)=0.42=0.16,P(X=3)=
×0.4×0.6×0.4=0.192,
P(X=4)=
×0.4×0.62+0.63=0.648.…(11分)
∴X的分布列为:
E(X)=2×0.16+3×0.192+4×0.648=3.488.…(13分)
则成绩在[80,90)范围内的人数是0.28×50=14人…(3分)
(Ⅱ)∵成绩在[80,90)范围内的频率是0.28,在[90,100)范围内的频率是0.12,
∴p=0.28+0.12=0.4.…(5分)
(i)该同学恰好答满4道题而获得一等奖,即前3道题中刚好答对1道,
第4道也能够答对才获得一等奖,
则有
| C | 1 3 |
∴该同学恰好答满4道题而获得一等奖的概率为0.1728.…(7分)
(ii)由题设可知,该同学答题个数为2、3、4.即X=2、3、4,
P(X=2)=0.42=0.16,P(X=3)=
| C | 1 2 |
P(X=4)=
| C | 1 3 |
∴X的分布列为:
| X | 2 | 3 | 4 |
| P | 0.16 | 0.192 | 0.648 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要注意频率分布直方图的合理运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
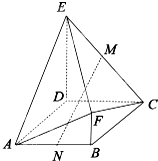 多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=
多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=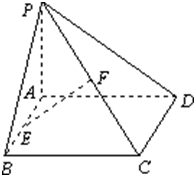 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD. 如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=
如图,四面体ABCD中,平面ABC⊥平面BCD,AC=AB,CB=CD,∠DCB=120°.点E在BD上,且DE=