题目内容
已知抛物线y2=4x的焦点F1与中心在原点的椭圆C的右焦点重合,且椭圆C过点(1,
).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点F1作直线l与椭圆C交于A、B两点,且点T是x轴上的一点,横坐标为2,求|
+
|的取值范围.
| ||
| 2 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点F1作直线l与椭圆C交于A、B两点,且点T是x轴上的一点,横坐标为2,求|
| TA |
| TB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由抛物线y2=4x可得焦点F1(1,0),可得椭圆的半焦距c=1.设椭圆的标准方程为
+
=1(a>b>0),把点(1,
)代入可得:
+
=1,又a2=b2+1,即可解得;
(II)(i)当直线l的斜率不存在时,可得A(1,
),B(1,-
),又T(2,0),即可得出|
+
|=2.
(ii)当直线l的斜率存在时,设直线l的方程为y=k(x-1),与椭圆的方程联立可化为(1+2k2)x2-4k2x+2k2-2=0,设A(x1,y1),B(x2,y2),可得根与系数的关系.又
=(x1-2,y1),
=(x2-2,y2),即可得出|
+
|2=(x1+x2-4)2+(y1+y2)2,代入换元再利用二次函数的单调性即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 1 |
| a2 |
| 1 |
| 2b2 |
(II)(i)当直线l的斜率不存在时,可得A(1,
| ||
| 2 |
| ||
| 2 |
| TA |
| TB |
(ii)当直线l的斜率存在时,设直线l的方程为y=k(x-1),与椭圆的方程联立可化为(1+2k2)x2-4k2x+2k2-2=0,设A(x1,y1),B(x2,y2),可得根与系数的关系.又
| TA |
| TB |
| TA |
| TB |
解答:
解:(I)∵抛物线y2=4x的焦点F1(1,0)与中心在原点的椭圆C的右焦点重合,
∴椭圆的半焦距c=1.
设椭圆的标准方程为
+
=1(a>b>0),
把点(1,
)代入可得:
+
=1,又a2=b2+1,
解得a2=2,b2=1,
∴椭圆C的标准方程为
+y2=1.
(II)(i)当直线l的斜率不存在时,可得A(1,
),B(1,-
),又T(2,0),
∴|
+
|=|(-1,
)+(-1,-
)|=|(-2,0)|=2.
(ii)当直线l的斜率存在时,设直线l的方程为y=k(x-1),
联立
,化为(1+2k2)x2-4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
∵
=(x1-2,y1),
=(x2-2,y2),
∴
+
=(x1+x2-4,y1+y2),
∴|
+
|2=(x1+x2-4)2+(y1+y2)2
=
+
=4+
+
,
令t=
,可知t∈(0,1].
∴|
+
|2=2t2+10t+4=2(t+
)2-
∈(4,16],
∴|
+
|∈(2,4].
综上可得:|
+
|∈[2,4].
∴椭圆的半焦距c=1.
设椭圆的标准方程为
| x2 |
| a2 |
| y2 |
| b2 |
把点(1,
| ||
| 2 |
| 1 |
| a2 |
| 1 |
| 2b2 |
解得a2=2,b2=1,
∴椭圆C的标准方程为
| x2 |
| 2 |
(II)(i)当直线l的斜率不存在时,可得A(1,
| ||
| 2 |
| ||
| 2 |
∴|
| TA |
| TB |
| ||
| 2 |
| ||
| 2 |
(ii)当直线l的斜率存在时,设直线l的方程为y=k(x-1),
联立
|
设A(x1,y1),B(x2,y2),则x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
∵
| TA |
| TB |
∴
| TA |
| TB |
∴|
| TA |
| TB |
=
| 16(1+k2)2 |
| (1+2k2)2 |
| 4k2 |
| (1+2k2)2 |
=4+
| 10 |
| 1+2k2 |
| 2 |
| (1+2k2)2 |
令t=
| 1 |
| 1+2k2 |
∴|
| TA |
| TB |
| 5 |
| 2 |
| 17 |
| 2 |
∴|
| TA |
| TB |
综上可得:|
| TA |
| TB |
点评:本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题、向量的坐标运算及其数量积的性质、二次函数的单调性等基础知识与基本技能方法,考查了换元法、分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
下列三句话按三段论的模式排列顺序正确的是( )
①2012能被2整除;
②一切偶数都能被2整除;
③2012是偶数.
①2012能被2整除;
②一切偶数都能被2整除;
③2012是偶数.
| A、①②③ | B、②①③ |
| C、②③① | D、③②① |
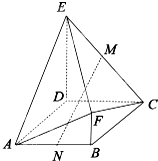 多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=
多面体ABCDEF中,M、N分别为EC、AB的中点,底面ABCD为菱形,且∠BAD=