题目内容
设两数列{an}、{bn}分别满足an+1=an+2n,bn+1=bn+2(n∈N+),且a1=b1=1.
(1)求数列{an}的通项公式;
(2)求数列{
}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)求数列{
| 1 |
| an+bn |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由数列递推式利用累加法求数列{an}的通项公式;
(2)求出等差数列{bn}的通项公式,代入
,整理后用裂项相消法求数列{
}的前n项和Sn.
(2)求出等差数列{bn}的通项公式,代入
| 1 |
| an+bn |
| 1 |
| an+bn |
解答:
解:(1)由an+1=an+2n,得an+1-an=2n,
则a2-a1=2×1.
a3-a2=2×2.
a4-a3=2×3.
…
an-an-1=2(n-1)(n≥2).
累加得:an-a1=2[1+2+3+…+(n-1)](n≥2),
∵a1=1,
∴an=1+2×
=n2-n+1 (n≥2).
验证n=1时成立.
∴an=n2-n+1;
(2)由bn+1=bn+2,即bn+1-bn=2,且b1=1,
∴bn=b1+(n-1)d=1+2(n-1)=2n-1.
则
=
=
=
-
,
∴Sn=(1-
)+(
-
)+(
-
)+…+(
-
)
=1-
=
.
则a2-a1=2×1.
a3-a2=2×2.
a4-a3=2×3.
…
an-an-1=2(n-1)(n≥2).
累加得:an-a1=2[1+2+3+…+(n-1)](n≥2),
∵a1=1,
∴an=1+2×
| (1+n-1)(n-1) |
| 2 |
验证n=1时成立.
∴an=n2-n+1;
(2)由bn+1=bn+2,即bn+1-bn=2,且b1=1,
∴bn=b1+(n-1)d=1+2(n-1)=2n-1.
则
| 1 |
| an+bn |
| 1 |
| n2-n+1+2n-1 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴Sn=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
| n |
| n+1 |
点评:本题考查了由累加法求数列的通项公式,训练了裂项相消法求数列的前n项和,是中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
若集合M=(y|y=x2-2x+1},N={x|y=x+
+2},则M与N的关系是( )
| 2x |
| A、M=N | B、M≠N |
| C、M∈N | D、M⊆N |
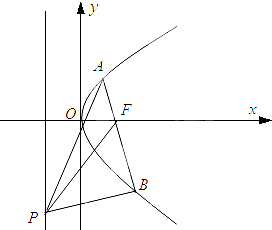 已知抛物线y2=2px(p>0)上点M(3,m)到焦点F的距离为4.
已知抛物线y2=2px(p>0)上点M(3,m)到焦点F的距离为4.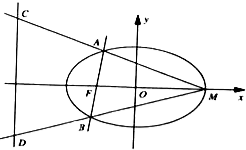 已知椭圆
已知椭圆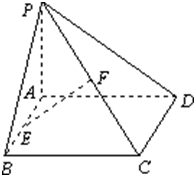 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.